Data Mining or knowledge discovery
SYNOPSIS
- INTRODUCTION
Data mining is the process of analyzing data from different perspectives and summarizing it into useful information. Data mining or knowledge discovery, is the computed assisted process of digging through and analyzing enormous sets of data and then extracting the meaning of data. Data sets of very high dimensionality, such as microarray data, pose great challenges on efficient processing to most existing data mining algorithms. Data management in high dimensional spaces presents complications, such as the degradation of query processing performance, a phenomenon also known as the curse of dimensionality.
Dimension Reduction (DR) tackles this problem, by conveniently embedding data from high dimensional to lower dimensional spaces. The dimensional reduction approach gives an optimal solution for the analysis of these high dimensional data. The reduction process is the action of diminishing the variable count to few categories. The reduced variables are new defined variables which are the combinations of either linear or non-linear combinations of variables. The reduction of variables to a clear dimension or categorization is extracted from the unusual dimensions, spaces, classes and variables.
Dimensionality reduction is considered as a powerful approach for thinning the high dimensional data. Traditional statistical approaches partly calls off due to the increase in the number of observations mainly due to the increase in the number of variables correlated with each observation. Dimensionality reduction is the transformation of High Dimensional Data (HDD) into a meaningful representation of reduced dimensionality. Principal Pattern Analysis (PPA) is developed which encapsulates feature extraction and feature categorization.
Multi-level Mahalanobis-based Dimensionality Reduction (MMDR), which is able to reduce the number of dimensions while keeping the precision high and able to effectively handle large datasets. The goal of this research is to discover the protein fold by considering both the sequential information and the 3D folding of the structural information. In addition, the proposed approach diminishes the error rate, significant rise in the throughput, reduction in missing of items and finally the patterns are classified.
- THESIS CONTRIBUTIONS AND ORGANIZATION
One aspect of the dimensionality reduction requires more studies to find out how the evaluations are performed. Researchers find to finish the evaluation with a sufficient understanding of the reduction techniques so that they can make a decision to use its suitability of the context. The main contribution of the work presented in this research is to diminish the high dimensional data into the optimized category variables also called reduced variables. Some optimization algorithms have been used with the dimensionality reduction technique in order to get the optimized result in the mining process.
The optimization algorithm diminishes the noise (any data that has been received, stored or changed in such a manner that it cannot be read or used by the program) in the datasets and the dimensionality reduction diminishes the large data sets to the definable data and after that if the clustering process is applied, the clustering or any mining results will yield the efficient results.
The organization of the thesis is as follows:
Chapter 2 presents literature review on the dimensionality reduction and protein folding as application of the research. At the end all the reduction technology has been analyzed and discussed.
Chapter 3 presents the dimensionality reduction with PCA. In this chapter some hypothesis has been proved and the experimental results has been given for the different dataset and compared with the existing approach.
Chapter 4 presents the study of the Principal Pattern Analysis (PPA). It presents the investigation of the PPA with other dimensionality reduction phase. So by the experimental result the obtained PPA shows better performance with other optimization algorithms.
Chapter 5 presents the study of PPA with Genetic Algorithm (GA). In this chapter, the procedure for protein folding in GA optimization has been given and the experimental result shows the accuracy and error rate with the datasets.
Chapter 6 presents the results and discussion of the proposed methodology. The Experimental results shows that PPA-GA gives better performance compared than the existing approaches.
Chapter 7 concludes our research work with the limitation which the analysis has been made from our research and explained about the extension of our research so that how it could be taken to the next level of research.
- RELATED WORKS
(Jiang, et al. 2003) proposed a novel hybrid algorithm combining Genetic Algorithm (GA). It is crucial to know the molecular basis of life for advances in biomedical and agricultural research. Proteins are a diverse class of biomolecules consisting of chains of amino acids by peptide bonds that perform vital functions in all living things. (Zhang, et al. 2007) published a paper about semi supervised dimensionality reduction. Dimensionality reduction is among the keys in mining high dimensional data. In this work, a simple but efficient algorithm called SSDR (Semi Supervised Dimensionality Reduction) was proposed, which can simultaneously preserve the structure of original high dimensional data.
(Geng, et al. 2005) proposed a supervised nonlinear dimensionality reduction for visualization and classification. Dimensionality reduction can be performed by keeping only the most important dimensions, i.e. the ones that hold the most useful information for the task at hand, or by projecting the original data into a lower dimensional space that is most expressive for the task. (Verleysen and François 2005) recommended a paper about the curse of dimensionality in data mining and time series prediction.
The difficulty in analyzing high dimensional data results from the conjunction of two effects. Working with high dimensional data means working with data that are embedded in high dimensional spaces. Principal Component Analysis (PCA) is the most traditional tool used for dimension reduction. PCA projects data on a lower dimensional space, choosing axes keeping the maximum of the data initial variance.
(Abdi and Williams 2010) proposed a paper about Principal Component Analysis (PCA). PCA is a multivariate technique that analyzes a data table in which observations are described by several inter-correlated quantitative dependent variables. The goal of PCA are to,
- Extract the most important information from the data table.
- Compress the size of the data set by keeping only this important information.
- Simplify the description of the data set.
- Analyze the structure of the observations and the variables.
In order to achieve these goals, PCA computes new variables called PCA which are obtained as linear combinations of the original variables. (Zou, et al. 2006) proposed a paper about the sparse Principal Component Analysis (PCA). PCA is widely used in data processing and dimensionality reduction. High dimensional spaces show surprising, counter intuitive geometrical properties that have a large influence on the performances of data analysis tools. (Freitas 2003) proposed a survey of evolutionary algorithms of data mining and knowledge discovery.
The use of GAs for attribute selection seems natural. The main reason is that the major source of difficulty in attribute selection is attribute interaction. Then, a simple GA, using conventional crossover and mutation operators, can be used to evolve the population of candidate solutions towards a good attribute subset. Dimension reduction, as the name suggests, is an algorithmic technique for reducing the dimensionality of data. The common approaches to dimensionality reduction fall into two main classes.
(Chatpatanasiri and Kijsirikul 2010) proposed a unified semi supervised dimensionality reduction framework for manifold learning. The goal of dimensionality reduction is to diminish complexity of input data while some desired intrinsic information of the data is preserved. (Liu, et al. 2009) proposed a paper about feature selection with dynamic mutual information. Feature selection plays an important role in data mining and pattern recognition, especially for large scale data.
Since data mining is capable of identifying new, potential and useful information from datasets, it has been widely used in many areas, such as decision support, pattern recognition and financial forecasts. Feature selection is the process of choosing a subset of the original feature spaces according to discrimination capability to improve the quality of data. Feature reduction refers to the study of methods for reducing the number of dimensions describing data. Its general purpose is to employ fewer features to represent data and reduce computational cost, without deteriorating discriminative capability.
(Upadhyay, et al. 2013) proposed a paper about the comparative analysis of various data stream procedures and various dimension reduction techniques. In this research, various data stream mining techniques and dimension reduction techniques have been evaluated on the basis of their usage, application parameters and working mechanism. (Shlens 2005) proposed a tutorial on Principal Component Analysis (PCA). PCA has been called one of the most valuable results from applied linear algebra. The goal of PCA is to compute the most meaningful basis to re-express a noisy data set.
(Hoque, et al. 2009) proposed an extended HP model for protein structure prediction. This paper proposed a detailed investigation of a lattice-based HP (Hydrophobic – Hydrophilic) model for ab initio Protein Structure Prediction (PSP). (Borgwardt, et al. 2005) recommended a paper about protein function prediction via graph kernels. Computational approaches to protein function prediction infer protein function by finding proteins with similar sequence. Simulating the molecular and atomic mechanisms that define the function of a protein is beyond the current knowledge of biochemistry and the capacity of available computational power.
(Cutello, et al. 2007) suggested an immune algorithm for Protein Structure Prediction (PSP) on lattice models. When cast as an optimization problem, the PSP can be seen as discovering a protein conformation with minimal energy. (Yamada, et al. 2011) proposed a paper about computationally sufficient dimension reduction via squared-loss mutual information. The purpose of Sufficient Dimension Reduction (SDR) is to find a low dimensional expression of input features that is sufficient for predicting output values. (Yamada, et al. 2011) proposed a sufficient component analysis for SDR. In this research, they proposed a novel distribution free SDR method called Sufficient Component Analysis (SCA), which is computationally more efficient than existing methods.
(Chen and Lin 2012) proposed a paper about feature aware Label Space Dimension Reduction (LSDR) for multi-label classification. LSDR is an efficient and effective paradigm for multi-label classification with many classes. (Brahma 2012) suggested a study of algorithms for dimensionality reduction. Dimensionality reduction refers to the problems associated with multivariate data analysis as the dimensionality increases.
There are huge mathematical challenges has to be encountered with high dimensional datasets. (Zhang, et al. 2013) proposed a framework to inject the information of strong views into weak ones. Many real applications involve more than one modal of data and abundant data with multiple views are at hand. Traditional dimensionality reduction methods can be classified into supervised or unsupervised, depending on whether the label information is used or not.
(Danubianu and Pentiuc 2013) proposed a paper about data dimensionality reduction framework for data mining. The high dimensionality of data can cause also data overload, and make some data mining algorithms non applicable. Data mining involves the application of algorithms able to detect patterns or rules with a specific means from large amounts of data, and represents one step in knowledge discovery in database process.
-
OBJECTIVES AND SCOPE
- OBJECTIVES
Generallydimension reduction is the process of reduction of concentrated random variable where it can be divided into feature selection and feature extraction. The dimension of the data depends on the number of variables that are measured on each investigation. While scrutinizing the statistical records data accumulated in an exceptional speed, so dimensionality reduction is an adequate approach for diluting the data.
While working with this reduced representation, tasks such as clustering or classification can often yield more accurate and readily illustratable results, further the computational costs may also be greatly diminished. A different algorithm called Principal Pattern Analysis (PPA) is presented in this research. Hereby the desire of dimension reduction is enclosed.
- The description of a diminished set of features.
- For a count of learning algorithms, the training and classification times increase precisely with the number of features.
-
Noisy or inappropriate features can have the same influence on the classification as predictive features, so they will impact negatively on accuracy.
- SCOPE
The scope of this research is to present an ensemble approach for dimensionality reduction along with pattern classification. Dimensionality reduction is the process of reduction the high dimensional data i.e., having the large features in the datasets which contain the complicated data. The usage of this dimensionality reduction process yields many useful and effective results over the process in mining. The former used many techniques to overcome this dimensionality reduction problem but they are having certain drawbacks to it.
The dimensional reduction technique enriches the execution time and yields the optimized result for the high dimensional data. So, the analysis states that before going for any clustering process, it is suggested for a dimensional reduction process of the high dimensional datasets. As in the case of dimensionality reduction, there are chances of missing the instruction. So the approach which is used to diminish the dimensions should be more corresponding to the whole datasets.
- RESEARCH METHODOLOGY
The scope of this research is to present an ensemble approach for dimensionality reduction along with the pattern classification. Problems on analyzing High Dimensional Data are,
- Curse of dimensionality
- Some important factors are missed
- Result is not accurate
- Result is having noise.
In order to mine the surplus data besides estimating gold nugget (decisions) from data involves several data mining techniques. Generally the dimension reduction is the process of reduction of concentrated random variables where it can be divided into feature selection and feature extraction.
- PRINCIPAL PATTERN ANALYSIS
The Principal Component Analysis decides the weightage of the respective dimension of a database. It is required to reduce the dimension of the data (having less features) in order to improve the efficiency and accuracy of data analysis. Traditional statistical methods partly calls off due to the increase in the number of observations, but mainly because of the increase in number of variables associated with each observation. As a consequence an ideal technique called Principal Pattern Analysis (PPA) is developed which encapsulates feature extraction and feature categorization. Initially it applies Principal Component Analysis (PCA) to extract Eigen vectors similarly to prove pattern categorization theorem the corresponding patterns are segregated.
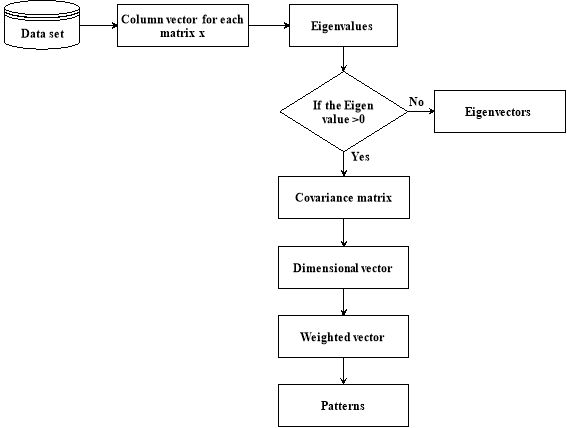
Figure.1. Architecture of Principal Pattern Analysis
Figure 1 represents the architecture of PPA process. PPA process’s steps are represented in the above diagram. The major difference between the PCA and PPA is the construction of the covariance matric. PPA algorithm for the dimensionality reduction along with the pattern classification has been introduced. The step by step procedure has been given as follows:
- Compute the column vectors such that each column is with M rows.
- Locate the column vectors into single matrix X of which each column has M x N dimensions. The empirical mean EX is computed for M x N dimensional matrix.
- Subsequently the correlation matric Cx is computed for M x N matrix.
- Consequently the Eigen values and Eigen vectors are calculated for X.
-
By interrupting the estimated results, the PPA algorithm persists by proving the Pattern Analysis theorem.
- FEATURE EXTRACTION
Feature extraction is an exception form of dimensionality reduction. It is needed when the input data for an algorithm is too large to be processed and it is suspected to be notoriously redundant then the input data will be transformed into a reduced representation set of features. By the way of explanation transforming the input data into the set of features is called feature extraction. It is expected that the feature set will extract the relevant information from the input data in order to perform the desired task using the reduced information of the full size input.
-
ESSENTIAL STATISTICS MEASURES
- CORRELATION MATRIX
A correlation matrix is used for pointing the simple correlation r, among all possible pairs of variables included in the analysis; also it is a lower triangle matrix. The diagonal elements are usually omitted.
- BARTLETT’S TEST OF SPHERICIY
Bartlett’s test of Sphericity is a test statistic used to examine the hypothesis that the variables are uncorrelated in the population. In other words, the population correlation matric is an identity matrix; each variable correlates perfectly with itself but has no correlation with the other variables.
- KAISER MEYER OLKIN (KMO)
KMO is a measure of sampling adequacy, which is an index. It is applied with the aim of examining the appropriateness of factor/Principal Component Analysis (PCA). High values indicate that factor analysis benefits and their value below 0.5 imply that factor suitable may not be suitable.
4.3.4MULTI-LEVEL MAHALANOBIS-BASED DIMENSIONALITY REDUCTION (MMDR)
Multi-level Mahalanobis-based Dimensionality Reduction (MMDR), which is able to reduce the number of dimensions while keeping the precision high and able to effectively handle large datasets.
- MERITS OF PPA
The advantages of PPA over PCA are,
- Important features are not missed.
- Error approximation rate is also very less.
- It can be applied to high dimensional dataset.
- Moreover, features are extracted successfully which also gives a pattern categorization.
- CRITERION BASED TWO DIMENSIOANL PROTEIN FOLDING USING EXTENDED GA
Extensively, protein folding is the method by which a protein structure deduces its functional conformation. Proteins are folded and held bonded by several forms of molecular interactions. Those interactions include the thermodynamic constancy of the complex structure, hydrophobic interactions and the disulphide binders that are formed in proteins. Folding of protein is an intricate and abstruse mechanism. While solving protein folding prediction, the proposed work incorporates Extended Genetic Algorithm with Concealed Markov Model (CMM).
The proposed approach incorporates multiple techniques to achieve the goal of protein folding. The steps are,
- Modified Bayesian Classification
- Concealed Markov Model (CMM)
- Criterion based optimization
- Extended Genetic Algorithm (EGA).
4.4.1MODIFIED BAYESIAN CLASSIFICATION
Modified Bayesian classification method is used grouping of protein sequence into its related domains such as Myoglobin, T4-Lysozyme and H-RAS etc. In Bayesian classification, data is defined by the probability distribution. Probability is calculated that the data element ‘A’ is a member of classes C, where C = {C1, C2 … CN}.
 (1)
(1)
Where, Pc(A) is given as the density of the class C evaluated at each data element.
Order Now