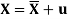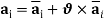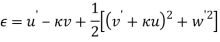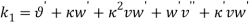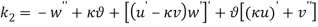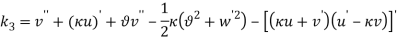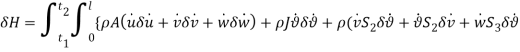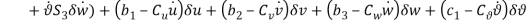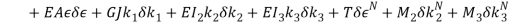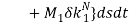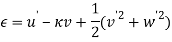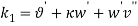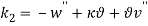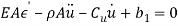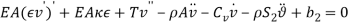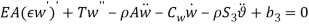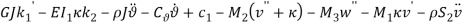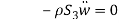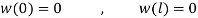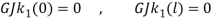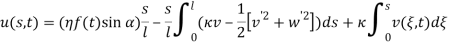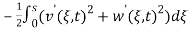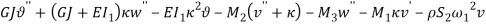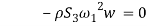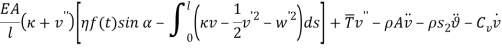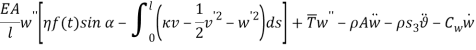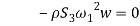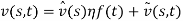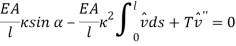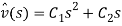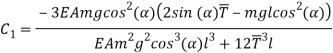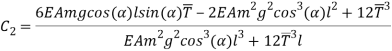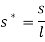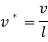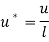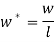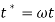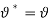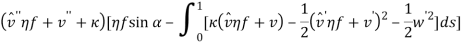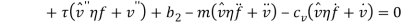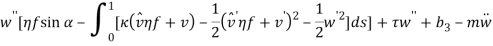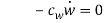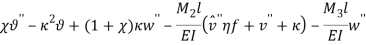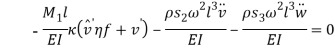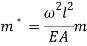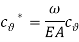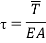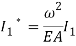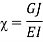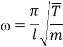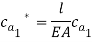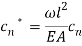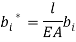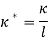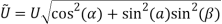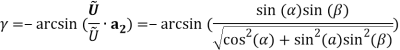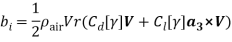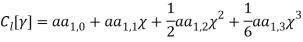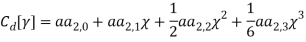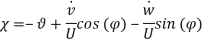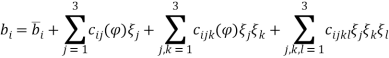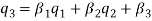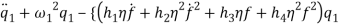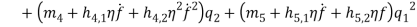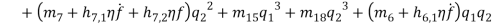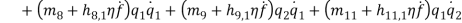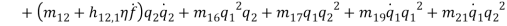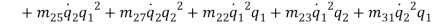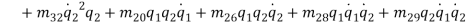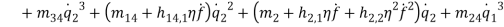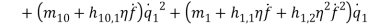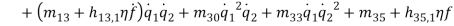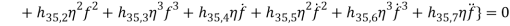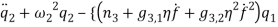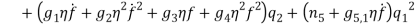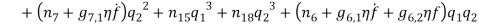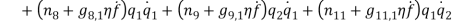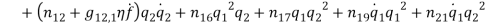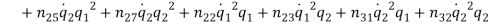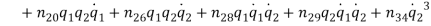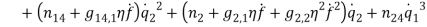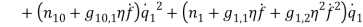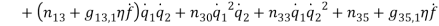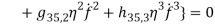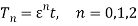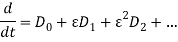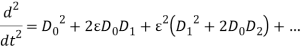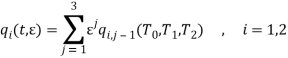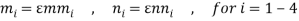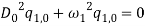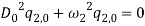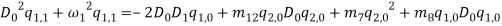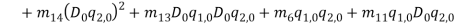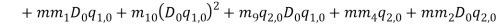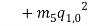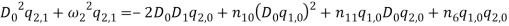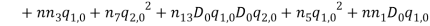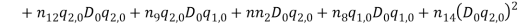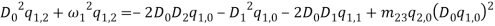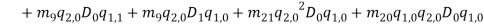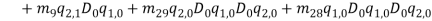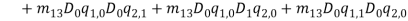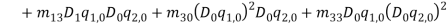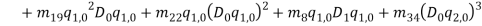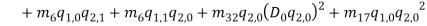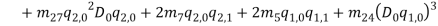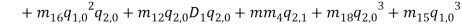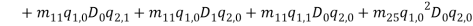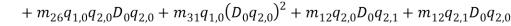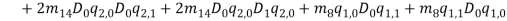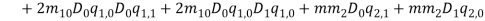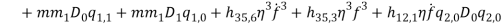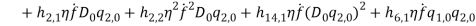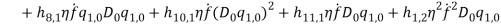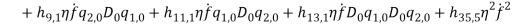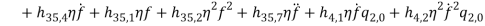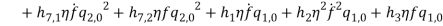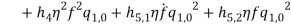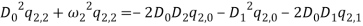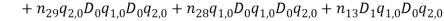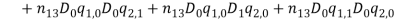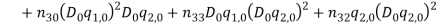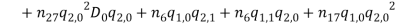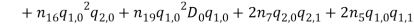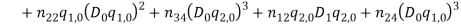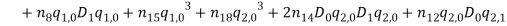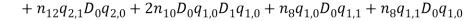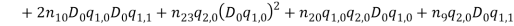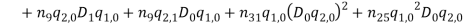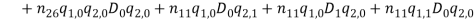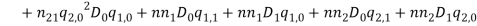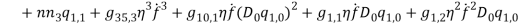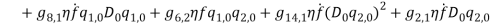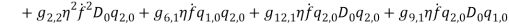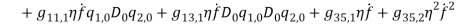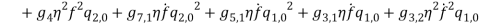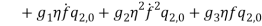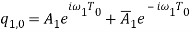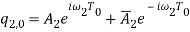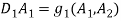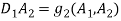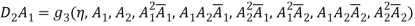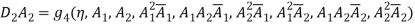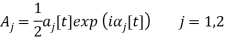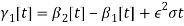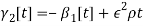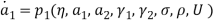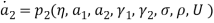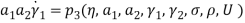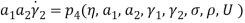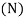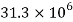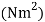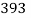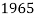Effect of Eccentricity on Nonlinear Galloping of Cables
The Effect of Eccentricity on the Nonlinear Galloping of Cables under Combined Wind Flow and Support motion in 1:1 Internal, External and Parametric Resonance Condition
Amir Jalali Saman Sadripour
Department of Mechanical Engineering, Shahrood University of Technology, Shahrood, Iran.
Galloping of cables is a kind of self-excited vibration and characterized with high amplitude and low frequency. In this paper for investigating the nonlinear galloping of an inclined cable, considering flexural and torsional stiffness, a cable-beam model is used. The iced cable is formulated under the effects of combined wind flow and support motion. Assuming low sag to span ratio and using physical parameter values of the cable, the governing equation of motion is obtained as a classical equations of the perfectly flexible cable, plus a further equation governing the twist motion. These two degrees of freedom system is discretized via the Galerkin method, by taking one in-plane and one out-of-plane modes as trial function. Two resulting non-homogeneous ordinary differential equations are coupled and contain quadratic and cubic nonlinearities in both velocity and displacement terms. By using multiple scale method for 1:1 internal resonance and 1:1 external resonance, a first order amplitude-phase modulation equation, governing the slow dynamic of the cable, is obtained. In this paper the wind speed and the eccentricity of the iced section are set as control parameters. Without consideration the eccentricity, the value of amplitude is increased as the wind speed is increase. But considering the eccentricity reduced to firstly increasing and then decreasing the amplitude.
Keywords:Galloping, Stiff Cable, Wind Flow, Eccentricity, Perturbation method
- Introduction
Cables are light and flexible structures which are used commonly in many engineering structures. Because of their low inherent damping, Cables are exposed to wind-induced vibration. Galloping is a classic phenomenon of aerodynamic instability of slender structures having non-circular cross sections [analytical]. A circular cylinder, with perfect symmetry will not exhibit galloping, though galloping is a common occurrence of on ice-laden cables, where the ice introduces the required asymmetry [1]. Galloping is characterized by low frequency and high amplitude vibration and has many roles in the field of cable vibration. The effects of galloping on a transmission line is dependent upon the severity and duration of the galloping event but typical problems are phase to phase flashover causing outages and arcing damage to conductors, loosening of tower bolts and damage to suspension and tension clamps, spacers and vibration dampers and, in some critical cases, structural damage to towers [1]. In order to prevent these damages, it is important to study on this kind of vibration.
The initial galloping model was proposed by Irvine [1], this model is based on the low sag to span ratio. The first studies of galloping considered it to be single degree of freedom (mono-modal galloping); Den Hartog [1] and Parkinson [1] introduce a model by consideration the vertical direction for galloping motion. Jones [1] and Luongo [1] proposed a two degree of freedom model by consideration vertical and horizontal motion and the interaction between them. In a major advance in (2010) Blevins [1] and Yu et al. [1] analyzed the effect of rotation on galloping and have found that the rotation plays an important role on the initiation of galloping under certain conditions. After that Yu [1, 2] proposed a three degree of freedom galloping model (vertical, horizontal and rotational) by consideration eccentricity of ice. The 3-DOF models have been used widely in galloping analysis using analytical and finite element methods. All these models consider the cable as a flexible structure and cannot consider the bending effects. Luongo [10-12] proposed a new model for considering both bending and rotation. This new model is based on the curved-beam theory and importance of consideration bending effects has been proved in linear [1] and nonlinear regime [1] under internal resonance conditions, devoting attention to the comparison between analytical and numerical approaches [1].
In the present paper, to investigate the effect of eccentricity on the iced cables which exposed to wind flow and support motion simultaneously, a nonlinear curved beam model [1] is introduced. The proposed model in this paper, is a nonlinear model of an inclined cable which able to twist and displacement in three normal, bi-normal and tangential directions. By using strain-displacements relation and based on Hamilton principle equations of motion can be derived. The aerodynamic forces are modeled referring to the quasi-steady theory, and they depend on the mean wind speed and on the angle of attack. Moreover, according to the property of the sample cable and Galerkin method, by considering one in-plane and one out-of-plane modes, a simplified two-degree of-freedom (normal and bi-normal) model with consideration of torsion, bending and eccentricity has been obtained. The two resulting equations are second order, non-homogeneous, time-periodic, ordinary differential equations and coupled with quadratic and cubic nonlinearities, both in the displacements and velocities. By using multiple scale method for 1:1 internal resonance between the in-plane and out-of-plane modes, and 1:1 external resonance between forcing and natural frequencies, a first order amplitude-phase modulation equation, governing the slow dynamic of the cable, is obtained. In this paper the wind speed, the eccentricity of the iced section and the amplitude of the support motion are set as control parameters.
The paper is organized as follows:
In the section 2 the equations of motion are formulated based on Hamiltonian theory. The reduced equations of motion are derived with simplifying assumption in section 3. By defining the non-dimensional parameters, Dimensionless equations are obtained in section 4. In the section 5 aerodynamic forces are formulated based on quasi-steady theory. Discretizing via Galerkin procedure is performed in the next section and the perturbation analysis is carried out in section 7, where the amplitude modulation equations are derived. Finally for a sample system, some conclusions are drawn in section 8.
- Mechanical model
The cable is modeled as a body made of a flexible centerline and rigid cross-sections restrained to remain orthogonal to the axis (shear-undeformable beam). It is assumed to be uniformly iced and loaded by a wind flow of mean velocity 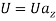 , blowing horizontally. For better description of cable-beam model, the choice of coordinates is made as following: directions 1,2 and 3 denote tangential, normal and bi-normal directions of transmission line, respectively. Four different configurations are considered. (a) the
, blowing horizontally. For better description of cable-beam model, the choice of coordinates is made as following: directions 1,2 and 3 denote tangential, normal and bi-normal directions of transmission line, respectively. Four different configurations are considered. (a) the 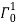 configuration, taken by the body at time
configuration, taken by the body at time 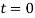 and the cable is under the action of gravity including ice, in this configuration the cable is in a vertical plane belong to (x,y) plane so the cross-section is in the (y,z) plane. (b) the
and the cable is under the action of gravity including ice, in this configuration the cable is in a vertical plane belong to (x,y) plane so the cross-section is in the (y,z) plane. (b) the 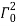 configuration, in this configuration the eccentricity of cross-section due to ice layer is considered. Because of eccentricity of iced transmission line, the configuration
configuration, in this configuration the eccentricity of cross-section due to ice layer is considered. Because of eccentricity of iced transmission line, the configuration 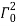 rotates the initial angle
rotates the initial angle 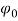 from shape
from shape 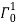 . (c) the reference configuration
. (c) the reference configuration 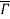 is considered by the body at time
is considered by the body at time 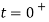 , it is assumed in which static aerodynamic forces act on transmission line. Due to static aerodynamic forces the cross section rotates the angle
, it is assumed in which static aerodynamic forces act on transmission line. Due to static aerodynamic forces the cross section rotates the angle 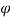 from the shape
from the shape 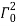 , this configuration is described by planner curve
, this configuration is described by planner curve 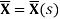 and by the cross-section inertial principal triad
and by the cross-section inertial principal triad 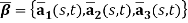 assumed to be coincident with the Frenet triad [1]. (d) the actual configuration
assumed to be coincident with the Frenet triad [1]. (d) the actual configuration 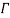 is considered at time
is considered at time 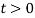 , it is assumed all forces including static and dynamic forces and support motion act on the body, The actual configuration of the body is described by the non-planar curve
, it is assumed all forces including static and dynamic forces and support motion act on the body, The actual configuration of the body is described by the non-planar curve 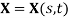 and the inertial principal triad
and the inertial principal triad 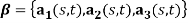 . Because of the dynamic part of aerodynamic force, the dynamic rotation and transport is described by
. Because of the dynamic part of aerodynamic force, the dynamic rotation and transport is described by 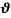 and the displacement vector field
and the displacement vector field 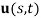 , respectively.
, respectively.
|
|
(1) |
|
|
(2) |
According to [2, 3], assuming low sag to span ratio, the Lagrange strain-displacement relationship can be calculated as below:
|
|
(3) |
|
|
(4) |
|
|
(5) |
|
|
(6) |
Where 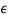 is stretching,
is stretching, 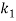 is torsion,
is torsion, 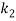 and
and 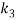 are bending strains, respectively and
are bending strains, respectively and 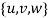 are the components of displacement vector
are the components of displacement vector 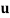 in basis
in basis 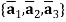 . “
. “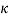 ” Is the initial curvature of the cable and “
” Is the initial curvature of the cable and “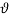 ” is the twist of the cross section. All the displacements and twist depends on the curvilinear abscissa “
” is the twist of the cross section. All the displacements and twist depends on the curvilinear abscissa “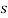 ” and time “
” and time “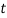 “. Based on [1] the equations of motion were derived via extended Hamilton principle by ignoring the shear resistance of the curved beam.
“. Based on [1] the equations of motion were derived via extended Hamilton principle by ignoring the shear resistance of the curved beam.
|
|
(7) |
Where 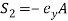 ;
; 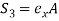 ;
; 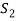 ,
, 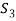 are the first moment of area about
are the first moment of area about 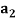 and
and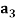 axes.
axes. 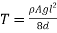 Is tensional,
Is tensional, 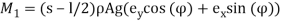 is the torsional,
is the torsional, 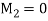 and
and 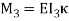 are the bending forces all at time “
are the bending forces all at time “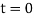 “. The sign ”.” denotes derivation with respect time “
“. The sign ”.” denotes derivation with respect time “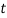 “;
“; 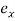 and
and 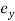 represent eccentricity of cross section about the
represent eccentricity of cross section about the 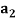 and
and 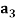 axes, respectively;
axes, respectively; 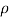 is the density of transmission line;
is the density of transmission line; 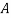 is the area of cross section;
is the area of cross section; 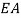 ,
, 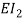 ,
, 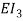 , and
, and 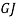 are the axial, bending and torsional stiffness, respectively;
are the axial, bending and torsional stiffness, respectively; 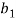 ,
, 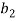 and
and 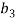 are aerodynamic forces;
are aerodynamic forces; 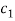 ,
, 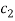 ,
, 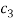 and
and 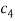 are structural damping coefficients;
are structural damping coefficients; 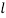 denotes the cable length.
denotes the cable length. 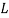 Represents the horizontal distance between adjacent towers;
Represents the horizontal distance between adjacent towers; 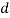 is sag at the mid-span.
is sag at the mid-span.
Based on [1] by reducing strain-displacement equations (1) – (1) to equations (1) – (1) and substituting them into equation (1), the equations of motion (1) – (1) with boundary condition (1) – (1) can be obtained in the four directions.
|
|
(8) |
|
|
(9) |
|
|
(10) |
|
Tangential direction: |
|
|
|
(11) |
|
Normal direction: |
|
|
|
(12) |
|
Bi-normal direction: |
|
|
|
(13) |
|
Torsional direction: |
|
|
|
(14) |
|
|
(15) |
|
|
(16) |
|
|
(17) |
|
|
(18) |
Where sign ” ´ ” denotes differentiation with respect to “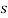 “.
“.
- Reduced equations of motion
Since the transversal-to-longitudinal (or torsional) squared frequency ratio is small, stretching and torsion are quasi-steady, so that inertial and damping forces can be neglected in the relevant equations. By substituting 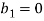 Longitudinal displacements are consequently statically condensed as (1) where the boundary conditions (1) have been used. Furthermore
Longitudinal displacements are consequently statically condensed as (1) where the boundary conditions (1) have been used. Furthermore 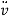 ,
, 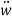 in equation (1) are assumed as
in equation (1) are assumed as 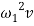 and
and 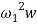 respectively. Thus equations (1) and (1) can be simplified as:
respectively. Thus equations (1) and (1) can be simplified as:
|
          |
(19) |
|
|
(20) |
According to the actual transmission line properties, 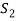 and
and 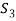 are very small compared with area of cable cross section
are very small compared with area of cable cross section 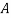 , therefore
, therefore 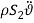 and
and 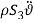 in equations (1) and (1) can be ignored. Since the equation in twist direction cannot be condensed such a simple way, it is convenient to use twist equation as an ancillary equation in the following. By substituting (1) in equations (1) to (1), the equations of motion can be obtained as equations (1) to (1) by boundary condition (1) to (1).
in equations (1) and (1) can be ignored. Since the equation in twist direction cannot be condensed such a simple way, it is convenient to use twist equation as an ancillary equation in the following. By substituting (1) in equations (1) to (1), the equations of motion can be obtained as equations (1) to (1) by boundary condition (1) to (1).
|
|
(21) |
|
|
(22) |
|
|
(23) |
|
|
(24) |
|
|
(25) |
|
|
(26) |
Since the equations of motion (1) to (1) have non-homogenous boundary conditions, by considering transformation (1) the system can be transform into an equivalent system with homogenous boundary condition.
|
|
(27) |
In which 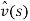 is quasi-static and
is quasi-static and 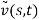 is dynamic component of the solution and they can be obtained by solving the linearized, non-homogenous system that is describe planner, linear, static of the cable, when a vertical unitary time-independent motion of the support is applied [1].
is dynamic component of the solution and they can be obtained by solving the linearized, non-homogenous system that is describe planner, linear, static of the cable, when a vertical unitary time-independent motion of the support is applied [1].
|
|
(28) |
|
|
(29) |
The particular solution of equation (1) can be obtained as follow:
|
|
(30) |
|
|
(31) |
|
|
(32) |
- Dimensionless form of equations
By defining non-dimensional parameter (1), dimensionless forms of equations of motion are obtained as follow:
|
|
|
|
|
|
|
|
|
|
|
(29) |
|
|
(30) |
|
|
(31) |
|
|
(32) |
In which all ‘*’ Superscripts have been eliminating in order to simplicity and non-dimensional parameters are introduced as follow:
|
|
|
|
|
|
|
|
|
|
|
|
|
(33) |
Where the index ‘n’ used instead of value 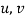 and
and 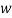 .
.
- Aerodynamic forces
In order to gain a simple aerodynamic model, simplifying assumption should be considered. a) The quasi-steady theory is adopted [1], b) the curvature of cable is neglected, c) the twist angle is accounted in loads but the effect of flexural rotation is neglected, d) the ice is uniformly cover the cable surface and e) the aerodynamic couples are neglected. Based on these assumptions aerodynamic forces 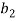 and
and 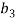 can be obtained. As shown in figure (1) wind blow with speed
can be obtained. As shown in figure (1) wind blow with speed 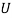 to cable plane, expression (1) denotes projection of this speed on the plane of cross section. The angle of attack introduced by the angle between direction of the component of wind speed on the cross section and a reference direction (hear the reference direction is adopted axis
to cable plane, expression (1) denotes projection of this speed on the plane of cross section. The angle of attack introduced by the angle between direction of the component of wind speed on the cross section and a reference direction (hear the reference direction is adopted axis 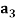 ), equation (1) and (1) express these concepts.
), equation (1) and (1) express these concepts.
|
|
(34) |
|
|
(35) |
Based on quasi-steady theory the aerodynamic force can be calculated by
|
|
(36) |
Where 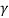 is angle of attack,
is angle of attack, 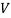 is the relative velocity between the wind speed and structure speed,
is the relative velocity between the wind speed and structure speed, 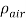 is air density,
is air density, 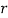 is characteristic radius of section,
is characteristic radius of section, 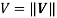 the modulus of relation speed,
the modulus of relation speed,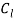 and
and 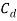 are lift and drag coefficient respectively and they’re dependent on the angle of attack and written as
are lift and drag coefficient respectively and they’re dependent on the angle of attack and written as
|
|
(37) |
|
|
(38) |
In which 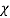 is defined as relation (1) and
is defined as relation (1) and 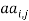 are the aerodynamic coefficients in reference configuration that are obtained by experimental results.
are the aerodynamic coefficients in reference configuration that are obtained by experimental results.
|
|
||
|
|
|
|
|
|
|
(39) |
By substituting these expression into (1) and projecting this equation on direction 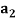 and
and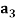 the components of aerodynamic force
the components of aerodynamic force 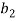 and
and 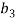 can be calculated as follow:
can be calculated as follow:
|
|
(40) |
For 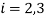 and where
and where 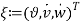 is a vector that collecting all the invariable components,
is a vector that collecting all the invariable components, 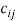 ,
, 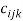 and
and 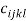 are the coefficients that depend on the
are the coefficients that depend on the 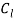 ,
, 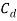 and their derivatives with respect to
and their derivatives with respect to 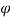 . The coefficients
. The coefficients 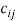 ,
, 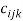 and
and 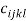 are reported in appendix.
are reported in appendix.
- Discrete model
In this section a discretization can be done via Galerkin procedure, by considering trial functions 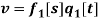 ,
, 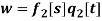 and
and 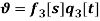 in which
in which 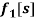 ,
, 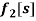 and
and 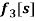 are normal, bi-normal and rotational mode shapes respectively and
are normal, bi-normal and rotational mode shapes respectively and 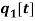 ,
, 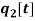 and
and 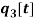 are normal, bi-normal and rotational amplitude varying as the time
are normal, bi-normal and rotational amplitude varying as the time 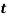 . By substituting these trial functions in equation (1), relation (1) is obtained. By considering relation (1) and substituting trial functions in equations (1) and (1) the discrete model is drown as (1) and (1).
. By substituting these trial functions in equation (1), relation (1) is obtained. By considering relation (1) and substituting trial functions in equations (1) and (1) the discrete model is drown as (1) and (1).
|
(41) |
|
|
(42) |
|
|
(43) |
|
Where 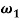 and
and 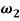 describe normal and bi-normal circular frequency of the iced cable respectively and coefficients
describe normal and bi-normal circular frequency of the iced cable respectively and coefficients 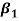 ,
, 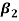 ,
, 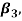
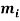 ,
, 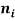 ,
, 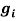 and
and 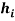 are reported in Appendix.
are reported in Appendix.
- Perturbation analysis
In order to investigate response of weakly nonlinear dynamic of iced cable, the method of multiple scales can be used. Since both quadratic and cubic terms exist in (1), three orders of perturbation equations are needed [1]. New time scales introduced such as (1) where 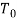 is fast and
is fast and 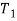 and
and 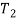 are slow time scales so that the first and second time-derivatives are expressed as (1) and The solutions are expanded in power series of
are slow time scales so that the first and second time-derivatives are expressed as (1) and The solutions are expanded in power series of 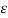 as written in (1) where
as written in (1) where 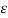 is dimensionless parameter (
is dimensionless parameter (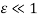 ).
).
|
|
(44) |
|
|
|
|
|
(45) |
|
|
(46) |
In this paper it is assumed that in-plane and out-of-plane natural frequency are in 1:1 ratio, 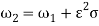 , it means that there is 1:1 internal resonance. The support motion assumed of sinusoidal type,
, it means that there is 1:1 internal resonance. The support motion assumed of sinusoidal type, 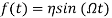 , in which
, in which 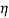 is the amplitude of motion and
is the amplitude of motion and 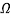 is the force frequency where assumed it is close to the natural ones so that a 1:1 external resonance occurs with both natural frequencies,
is the force frequency where assumed it is close to the natural ones so that a 1:1 external resonance occurs with both natural frequencies, 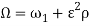 , where
, where 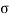 is internal and
is internal and 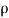 is external detuning parameters. Moreover, the coefficients
is external detuning parameters. Moreover, the coefficients 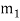 ,
, 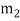 ,
, 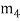 ,
, 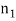 ,
, 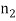 and
and 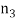 of equations (1) and (1) are assumed to be small as the same order of
of equations (1) and (1) are assumed to be small as the same order of 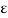 ,
, 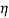 is assumed of order
is assumed of order 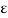 and all the coefficients are ordered so that the resonant external and parametric excitation terms appear at the highest order perturbation equations.
and all the coefficients are ordered so that the resonant external and parametric excitation terms appear at the highest order perturbation equations.
|
|
(47) |
By substituting equations (1) – (1) into equations (1) and (1) and collect them with powers of 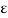 equations (1) – (1) are obtained.
equations (1) – (1) are obtained.
|
|
|
|
|
|
|
(48) |
|
|
|
|
|
|
|
|
(49) |
|
|
|
|
|
(50) |
|
|
(51) |
|
Equation (1) admits the solution (1), where 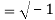 ,
, 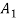 and
and 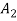 are unknown complex normal and bi-normal amplitudes depending on the slow time scales (
are unknown complex normal and bi-normal amplitudes depending on the slow time scales (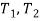 ) respectively,
) respectively, 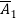 and
and 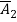 denote the complex conjugate of
denote the complex conjugate of 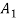 and
and 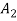 .
.
|
|
|
|
|
(52) |
Substitute 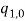 and
and 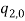 into equations of
into equations of 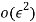 and
and 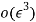 and eliminate secular terms equations (1) – (1) calculated.
and eliminate secular terms equations (1) – (1) calculated.
|
|
|
|
|
(53) |
|
|
|
|
|
(54) |
By defining polar form for 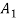 and
and 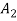 such as (1) where
such as (1) where 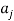 and
and 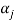 are amplitude and phase varying as time
are amplitude and phase varying as time 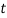 and definition (1) the amplitude modulation equations can be obtained as follow:
and definition (1) the amplitude modulation equations can be obtained as follow:
|
|
(55) |
|
|
|
|
(56) |
|
|
|
|
|
|
|
|
|
|
|
(57) |
- Numerical results and discussion
In order to numerically illustrate the cable model mentioned above, a sample U shaped iced cross section is considered (almost identical to the one presented in [1]), the cable properties mentioned in table (1). This model has axial rigidity 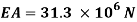 , torsional stiffness
, torsional stiffness 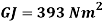 , bending stiffness
, bending stiffness 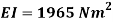 , mass per unit length (including ice)
, mass per unit length (including ice) 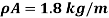 , the initial eccentricity along Y-axis
, the initial eccentricity along Y-axis 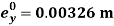 and initial rotation
and initial rotation 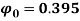 . It is assumed the cable has the length
. It is assumed the cable has the length 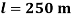 , and the sagÂÂ
, and the sag 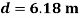 , according to these values the cable is close to the first cross over point [1] therefor the circular frequencies of normal displacement
, according to these values the cable is close to the first cross over point [1] therefor the circular frequencies of normal displacement 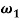 and bi-normal displacement
and bi-normal displacement 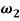 are calculated as
are calculated as 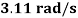 and
and 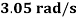 at the configuration
at the configuration 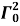
|
unit |
quantity |
sign |
parameter |
|
|
|
EA |
axial rigidity |
|
|
|
GJ |
torsional stiffness |
|
|
|
EI |
bending stiffness |
| Â |