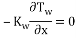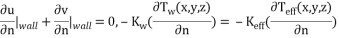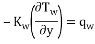Effect of Magnetic Field on Hydrodynamic Behavior
Effect of Magnetic Field on hydrodynamic behavior in a Microchannel Heat Sink
Mohammad Nasiri 1*, Mohammad Mehdi Rashidi 2,
1 Department Mechanical Engineering, Faculty of Mechanical Engineering, University of Tabriz, Tabriz 5166616471, Iran
2 Department of Civil Engineering, School of Engineering, University of Birmingham, Birmingham, UK.
ABSTRACT
In this study, hydrodynamic behavior nanofluid (Fe3O4-water) in a MicroChannel Heat Sink (MCHS) with Offset Fan Shaped under magnetic field was numerically investigated. The two phase mixture model was used to simulate the nanofluid flow. Flow was assumed laminar, steady and incompressible. The effects of changing Reynolds number, power magnetic field, and nanoparticle diameter on fluid behavior are considered. The results show that the friction factor decreases and Nusselt number enhances whit rising Reynolds number. Whit increases intensity magnetic field the pressure drop, friction factor and Nusselt number increasing. The results indicate that non-uniform magnetic field has more effect on nanofluid behavior compare uniform magnetic field.
Keywords
Nanofluid; Microchannel heat sink; Magnetic field; Friction factor; Nusselt number
|
Nomenclature |
|
|
|
Cartesian coordinate axes |
|
|
Velocity component in x and y and z direction, respectively (m/s) |
|
(a,b) |
Center of magnetic wire (m) |
|
|
Velocity vector (m/s) |
|
|
Velocity inlet (m/s) |
|
|
Acceleration vector (m/s2) |
|
|
Thermal conductivity (W/m K) |
|
|
Specific heat capacity at constant pressure |
|
|
(1.3806503Ã-10-23 J/K) |
|
|
Temperature (K) |
|
I |
Electric intensity (A) |
|
H |
Magnetic field intensity vector (A/m) |
|
|
Heat flux (1 MW/m2) |
|
|
Channel width (300Ã-10-6m) |
|
|
Hydraulic diameter (0.00001333 m) |
|
|
Channel length (2.70Ã-10-3m) |
|
|
Drag coefficient |
|
|
Mean velocity (m/s) |
|
|
Drift velocity (m/s) |
|
|
Slip velocity (m/s) |
|
d |
Mean diameter (nm) |
|
Nu= |
Nuselt number |
|
|
friction factor |
|
|
Reynolds number |
|
|
Prandtlnumber |
|
|
Magnetic field (T) |
|
Greek symbols |
|
|
|
magnetic permeability in vacuum (4ÀÃ-10-7 Tm/A) |
|
|
Dynamic viscosity (kg/m s) |
|
|
Thermal expansion coefficient(thermal expansion coefficient (K-1) |
|
|
Density (kg/m3) |
|
|
Mean free path (17Ã-10-9 m) |
|
|
Magnetic susceptibility |
|
|
Particle volume fraction |
|
|
Electrical conductivity (s/m) |
|
Subscripts |
|
|
|
Particle |
|
|
Base fluid |
|
bw |
Bottom wall |
|
|
Effective |
|
|
Average |
Introduction
Nanofluids has higher thermal conductivities compared to them base fluids [1-5]. Currently the use of nanofluids in thermal engineering systems such as heat exchangers [6-7], microchannels [8-10] , chillers, medical applications [11,12], and solar collectors [13].
Tsai and Chein[14] investigated analytically nanofluid (water-copper and nanotube) flow in microchannel heat sink. They was found that optimum values of aspect ratio and nanofluid did not make conversion in MCHS thermal resistance. Kalteh et al. [15] investigated the laminar nanofluid flow in rectangular microchannel heat sink both numerically and experimentally. Compared the experimental and numerical results presented that two-phase Eulerian-Eulerian method results are in better accordance with experimental results than the single-phase modeling. The reasons experimentally study by Azizi et al.[16] reported that Nusselt numbers decreases whit rising Reynolds number and enhancement heat transfer by using nanoparticles camper to that of pure water for similar Reynolds number. et al. [17] studied effect nanoparticle on heat transfer in a cavity square containing a rectangular heated body numerically. They indicated that using nanoparticle increasing heat transfer and dimensionless entropy generation.
Micro channel heat sink (MCHS) using in many applications, such as microelectronics and high energy laser. MCHS cooling is very important because heat flux in this channel higher than regular channel. Many studies analyzed the convective heat transfer characteristics of nanofluids in micro channel heat sink in recently many years ago[18-24].
Sakanova et al. [25] investigated effects of wavy channel structure on hydrodynamic behavior in microchannel heat sink. They found that increasing nanoparticles in pure water the effect of wavy wall unnoticeable. Radwan et al. [26] using nanofluid on heat transfer microchannel heat sink in low concentrated photovoltaic systems investigated numerically. They show that nanofluids is effective technique for enhance heat transfer. Tabrizi and Seyf [27] investigated laminar Al2O3-water nanofluid flow in a microchannel heat sink. They showed that increasing volume fraction of Al2O3 and nanoparticle size reducing the entropy generation.
Chai et al. [28-30] studied hydrothermal characteristics of laminar flow microchannel heat sink with fan-shaped ribs. Their results presented that used the fan-shaped ribs the average friction factor 1.1-8.28 times larger than the regular microchannel, while used the offset fan-shaped ribs was 1.22-6.27 times increases. Also the microchannel with large rib’s height and small rib’s spacing, the frictional entropy generation rate increases and thermal entropy generation rate decreases comparing than the smooth microchannel.
Magnetic fluid (ferrofluid) is a stable colloidal suspension consisting of a base liquid and magnetic nanoparticles that are coated with a surfactant layer and it can be controlled by external magnetic fields [31]. Sundar et al. [32-33] experimentally studied the heat transfer characteristic of Fe3O4 ferrofluid in a circular tube whit applied magnetic field. They detected that the heat transfer increases compared to water flow at same operating condition. Aminfar et al. [34-36] studied effect different magnetic field on ferrofluid for different channels. They showed that using the uniform and non-uniform transverse magnetic increasing heat transfer coefficient and friction factor. Also shown that non-uniform transverse magnetic enhanced heat transfer more than axial non-uniform magnetic field.
In this study, the uniform and non-uniform transverse magnetic effect on heat transfer of ferrofluids flow in a microchannel heat sink with offset fan shaped by using mixture model. The effects of uniform and non-uniform transverse power magnetic fields, Reynolds number and nanoparticle diameter variation are studied in details.
Governing Equations
Researchers presented different models for numerical analysis in multi-phase flows [37-40]. The mixture model is one of methods for nanofluid analyses [38-41]. In this study, flow is assumed steady state, incompressible and laminar with constant thermo-physical properties. The effects of body forces and dissipation are negligible. Also, for calculate the density variations due to buoyancy force was used the Boussinesq approximation. Considering these assumptions, the dimensional equations define as:
Continuity equations:
|
|
(1) |
Momentum equations:
|
|
(2) |
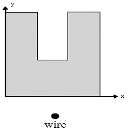
The term 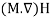 refers to Kelvin force; it results from the electric current flowing through the wire. In this equation, H is Magnetic field intensity vector that determined as [42]:
refers to Kelvin force; it results from the electric current flowing through the wire. In this equation, H is Magnetic field intensity vector that determined as [42]:
|
|
(3) |
where
|
|
(4) |
|
|
(5) |
I is electric intensity. The wire direction is parallel to the longitudinal channel and in the center of cross section at the (a, b).
Also, M is the magnetization in Equation (2) and determined as [36]:
|
|
(6) |
where 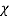 is magnetic susceptibility of ferrofluid at 4% volume fraction for different mean diameter is present in Table 1.
is magnetic susceptibility of ferrofluid at 4% volume fraction for different mean diameter is present in Table 1.
Table 1. magnetic susceptibility of ferrofluid for different mean diameter
|
mean diameter |
magnetic susceptibility |
|
10 |
0.34858668 |
|
20 |
2.7886935 |
|
30 |
9.4118388 |
In Equation (2), 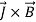 is called Lorentz force that determined as:
is called Lorentz force that determined as:
|
|
(7) |
Where 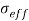 and
and 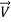 are respectively effective electrical conductivity and nanofluid velocity vector, also
are respectively effective electrical conductivity and nanofluid velocity vector, also 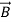 is the induced uniform magnetic field that can be calculated by intensity of magnetic field:
is the induced uniform magnetic field that can be calculated by intensity of magnetic field:
|
|
(8) |
Energy equation:
|
|
(9) |
Volume fraction equations:
|
|
(10) |
In Equation (10), Vm, and Vdr are the mean velocity and the drift velocity, respectively, that be defined as:
|
|
(11) |
|
|
(12) |
where Æis the volume fraction of nanoparticles.
The drift velocity depends on the slip velocity. The slip velocity defined as the velocity of base fluid (bf) with respect to velocity of nanoparticles (p) and determined as:
|
|
(13) |
|
|
(14) |
The slip velocity is presented by Manninen et al. [31e]:
|
|
(15) |
In Equation (15) f drag and r are drag coefficient and acceleration respectively, which can be calculated by:
|
|
(16) |
|
|
(17) |
In Equation (16), Rep = Vmdp/veff is the Reynolds number of particles.
Nanofluids Properties
The physical properties of water and Fe3O4 nano-particles are shown in Table 2. The water-Fe3O4 nanofluidis assumed is homogenous that the thermos-physical mixture properties calculated for 4% volume fraction of nanoparticles.
Table 2. Properties of base fluid and nanoparticles [35,40].
|
Properties |
Water |
Fe3O4 |
|
Density (kg/m3) |
997.1 |
5200 |
|
Specific heat capacity (J/kg∙K) |
4180 |
670 |
|
Thermal conductivity (W/m∙K) |
0.613 |
6 |
|
Electrical conductivity (s/m) |
5.3 |
25,000 |
|
Dynamic viscosity (kg/m∙s) |
0.0009963 |
– |
The physical mixture properties are calculated by means of the following equations:
Density of nanofluid:
|
|
(18) |
Specific heat capacity of the nanofluid:
|
|
(19) |
Dynamic viscosity of nanofluid [43]:
|
|
(20) |
Thermal expansion coefficient of nanofluid [35]:
|
|
(21) |
Electrical conductivity [36]:
|
|
(22) |
Based on the Brownian motion velocity is Thermal conductivity of nanofluid [44]:
|
|
(23) |
dp and dbf are particle diameter(nm) and molecular base fluid (0.2 nm).
In Equation (23) Pr and Re are Prandtl and Reynolds number, respectively defined as:
|
|
(24) |
|
|
(25) |
Also, in Equation (25) 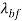 is water mean free path (17 nm) and kB is (1.3807 Ã- 10−23 J/K).
is water mean free path (17 nm) and kB is (1.3807 Ã- 10−23 J/K).
Deï¬Ânition of Physical Domain and numerical method
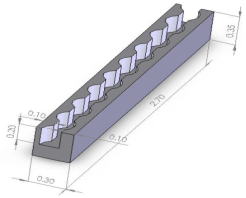
Fig.1 shown the geometry of the microchannel heat sink with offset fan-shaped reentrant cavities in sidewall. The channel width and space between a pair cavity is 300 μm.The channel length is 2.70 mm with a thickness of 350 μm and the pitch distance of two longitudinal microchannels is 150 μm.
The channel cross section heat sink has a constant width of 100 μm and constant depth of 200 μm and radius of the fan-shaped reentrant cavity is 100 μm.
|
|
|
|
|
|
a) |
b) |
|
|
|
c) |
|
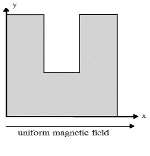
Fig. 1. a) Geometry of microchannel in the present study b) Cross-sectional plane of transverse non-uniform magnetic field c) Transverse uniform magnetic field
In this study, used the finite volume (FV) method to numerically solved non-linear partial differential equations. The velocity pressure coupling by SIMPLEC algorithm. The discretization of momentum and energy equations used the second order upwind scheme and the solid phase equations became discretization by first order scheme.
In this study for evaluate of effect the mesh points on the precision of the results, several grid sizes have been tested for the constant heat flux at Re = 300 are given in Table 3. The 1188000 grids is adequately suitable.
Table 3. Grid independent test (Re = 200,T0 = 300, 4% vol.).
|
V/V0 |
T/T0 |
Grid |
|
1.038 |
1.027 |
672914 |
|
1.029 |
1.019 |
889440 |
|
1.023 |
1.013 |
1188000 |
|
1.02 |
1.011 |
1591128 |
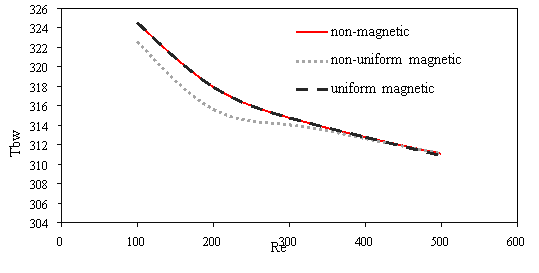
In order to validate this, the amount of mean temperature at the bottom of the microchannel compared by numerical result of Chai et al.[45](Fig.2). Also for comparison effect the magnetic field, the dimensionless velocity under the magnetic field compared by analytical results of Shercliff [46] that shown in Fig. 3 and can be seen a good agreement between results.
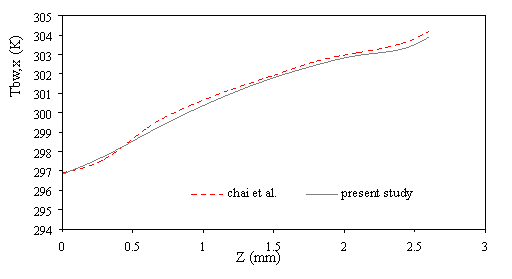
Figure 2. Comparison of the results for average temperature bottom heat sink
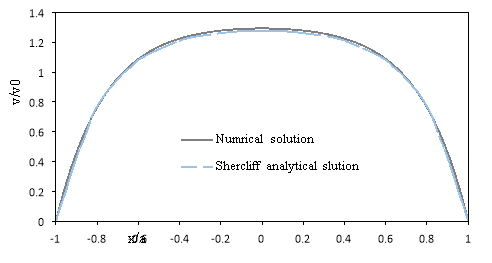
Fig.3 Comparison between numerical and analytical results for flow under magnetic field
Boundary conditions
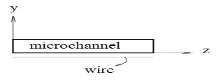
The set of non-linear elliptical governing equations are solved by using the boundary conditions in the entrance of microchannel (Z = 0),
|
u = 0; v = 0; w = v0 ; T = T0 |
(26) |
at the microchannel outlet (Z = 2.7 mm):
|
|
(27) |
In the left and right sides of microchannel outer adiabatic walls (X = 0 & w):
|
|
(28) |
In the microchannel inner walls:
|
|
(29) |
|
|
(30) |
Finally, a constant heat flux condition is imposed at micro heat sink bottom wall (y = 0).
Results and discussion
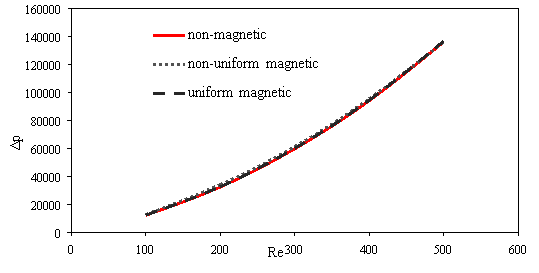
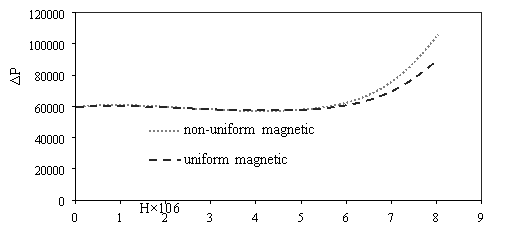
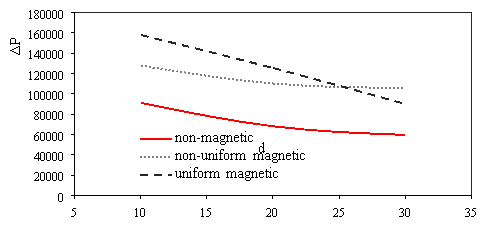
The variations of pressure drop and Reynolds number for various transverse magnetic fields are shown in Fig. 3a. It can be seen that for a given fluid, the pressure drop increases by increasing the Reynolds number because rising the velocity inlet. As shown in Fig. 3b whit increases intensity uniform and non-uniform magnetic field in the same Reynolds number (Re=300), the pressure drop increases for non-uniform magnetic because the secondary flow near wall became larger and powerful. Also scale up particle diameter of 10nm to 30nm decreasing pressure drop (Fig. 3c).
|
|
|
a) |
|
|
|
b) |
|
|
|
c) |
Fig. 3. Effects of various a) Reynolds number [H=6Ã-106, dp=30nm] b) power magnetic field gradients [Re=300, dp=30nm] c) particle diameter [H=8Ã-106, Re=300] on the pressure drop
Fig. 4 presented streamlines for various magnetic fields at 0.0015≤ Z ≤0.002. As shown in Fig.4, when magnetic field is weak the streamlines same together because the magnetic field had not enough powerful for veer stream. By increases intensity magnetic field the nanofluid flow shift to near wall and thereupon the vortex in reentrant cavities became powerful Fig.5.
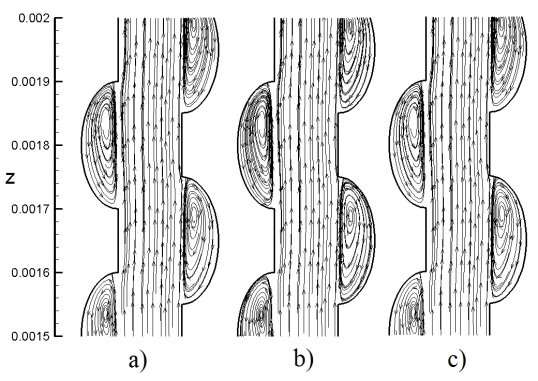
Fig. 4. Stream lines in same Reynolds number (Re=300) and particle diameter [dp= 30nm] for a) non-magnetic field b) non-uniform magnetic field (H=6Ã-106 A/m) c) uniform magnetic field (H=6Ã-106 A/m)

Fig. 5. Stream lines in same Reynolds number (Re=300) and particle diameter [dp= 30nm] for non-uniform magnetic field a) H= 6Ã-106 A/m c) H=8Ã-106 A/m
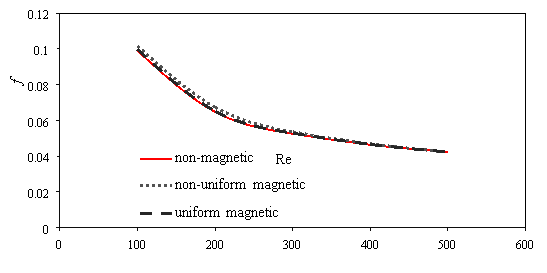
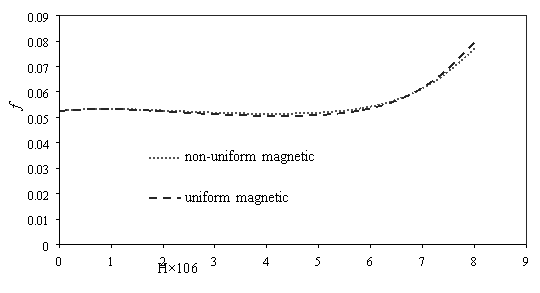
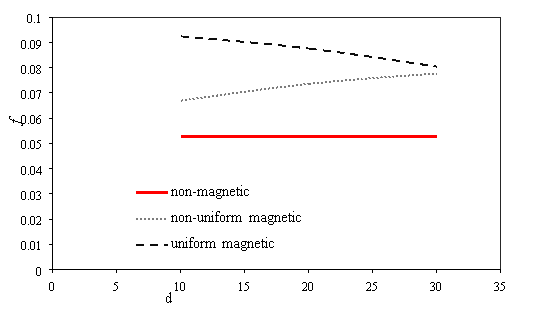
The friction factor decreases as Reynolds number increases (Fig. 6a). The magnetic field cannot overcome viscous force and affect mean velocity when intensity magnetic field is low, therefor the friction factor is almost fixed for using magnetic and non-magnetic field. Whit increases intensity magnetic field the mean velocity decreases and while the pressure drop increases (Fig. 3.b); therefore, the friction factor increases at maximum intensity field (Fig. 6b). Also scale up particle diameter the main velocity and pressure drop decreases. The uniform transverse magnetic field is depended to velocity that whit decreasing velocity the uniform transverse effect decreases on flow, so friction factor rising (Fig. 6c).
|
|
|
a) |
|
|
|
b) |
|
|
|
c) |
Fig. 6. Effects of various a) Reynolds number [H=6Ã-106, dp=30nm] b) power magnetic field gradients [Re=300, dp=30nm] c) particle diameter [H=8Ã-106, Re=300] on the friction factor
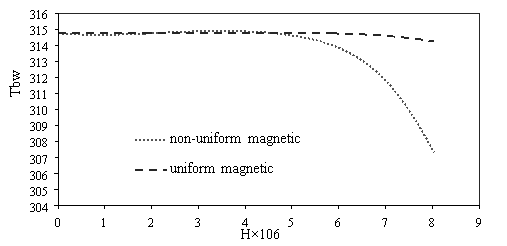
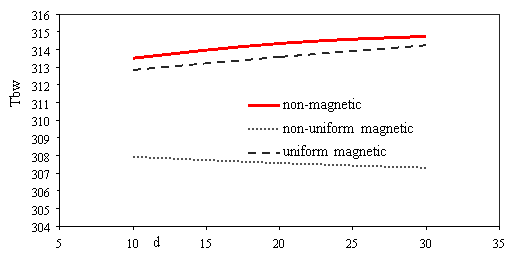
Figure 7 shows the variations of average temperature bottom heat sink for different condition. Whit increasing Reynolds numbers the velocity increasing too and the vortex in reentrant cavities became bigger and powerful, thus average temperature bottom heat sink decreases (Fig. 7a). Effects of various power magnetic field gradients [Re=300, dp=30nm] on average temperature bottom heat sink presented in Fig. 7b. When the intensity magnetic field is weak cannot affect average velocity because cannot overcome viscous force. By strengthening the non-uniform transverse magnetic field the average velocity became larger and growth vortex in channel, therefore average temperature bottom heat sink reduces. Particle diameter rising, the non-uniform transverse magnetic had more effect than uniform transverse magnetic and non-magnetic on average temperature bottom heat sink (Fig. 7c). Whit scale up particle diameter decreasing thermal conductivity and heat transfer for when applied uniform transverse magnetic because it independent of particle diameter.
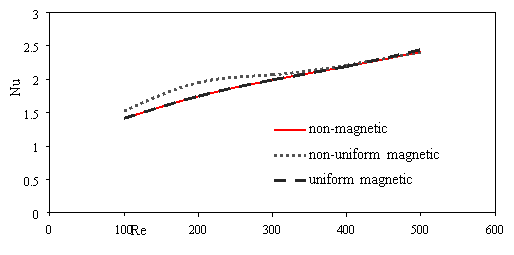
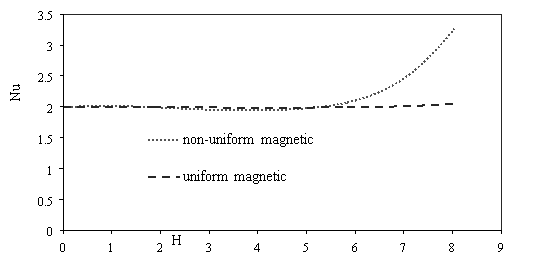
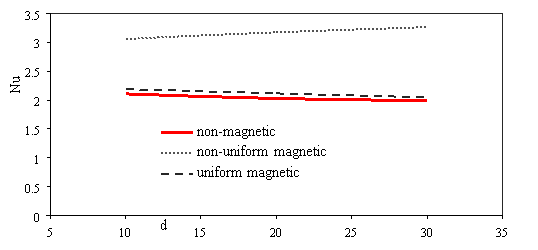
Figure 8 presented the variations of average Nusselt number for different condition. Nusselt number enhances with Reynolds number increases (Fig. 8a). In larger Reynolds number the magnetic field can’t conquest to viscosity force and shear stress, therefore the magnetic field hasn’t effect on nanofluid flow and should apply larger magnetic field. The same Reynolds [Re=300] number, non-uniform transverse magnetic has more effect than uniform transverse magnetic on heat transfer nanofluid flow (Fig. 8b). Figure 8c show the variations of average heat transfer for different particle diameter. When scale up particle diameter, increases effect non-uniform transverse magnetic on flow because depended to particle diameter.
|
|
|
a) |
|
|
|
b) |
|
|
|
c) |
Fig. 7. Effects of various a) Reynolds number [H=6Ã-106, dp=30nm] b) power magnetic field gradients [Re=300, dp=30nm] c) particle diameter [H=8Ã-106, Re=300] on average temperature bottom heat sink
|
|
|
a) |
|
|
|
b) |
|
|
|
c) |
Fig. 8. Effects of various a) Reynolds number [H=6Ã-106, dp=30nm] b) power magnetic field gradients [Re=300, dp=30nm] c) particle diameter [H=8Ã-106, Re=300] on average temperature bottom heat sink
Conclusions
In this study, the laminar nanofluid flow in a microchannel heat sink under transverse magnetic field is investigated. For numerically simulation used the two phase mixture models and finite volume method. When using the non-uniform magnetic field increasing the main heat transfer and friction factor almost fix by uniform magnetic field. When scale up particle diameter under non-uniform magnetic field the main heat transfer and friction factor increases but for apply uniform magnetic field main heat transfer.
Reference
[1] S.P. Jang, S.U.S. Choi, Role of Brownian motion in the enhanced thermal conductivity of nanofluids, Appl. Phys. Lett. 84 (2004) 4316-4318.
[2] B.X. Wang, L.P. Zhou, X.F. Peng, A fractal model for predicting the effective thermal conductivity of liquid with suspension of nanoparticles, Int. J. Heat Mass transfer 46 (2003) 2665-2672.
[3] Y. Xuan, Q. Li, W. Hu, Aggregation structure and thermal conductivity of nanofluids, AIChE J. 49 (4) (2003) 1038-1043.
[4] R. Prasher, P. Bhattacharya, P.E. Phelan, Thermal conductivity of nanoscale colloidal solutions (nanofluids), Phys. Rev. Lett. 94 (2) (2005) 025901.
[5] J. Koo, C. Kleinstreuer, Laminar nanofluid flow in microheat-sinks, Int. J. Heat Mass Transfer 48 (2005) 2652-2661.
[6] W. Duangthongsuk, S. Wongwises, Heat transfer enhancement and pressure drop characteristics of TiO2-water nanofluid in a double-tube counter flow heat exchanger, Int. J. Heat Mass Transfer 52 (7-8) (2009) 2059-2067.
[7] F. Garoosi, L. Jahanshaloo, M.M. Rashidi, A. Badakhsh, M.A. Ali, Numerical Simulation of Natural Convection of the Nanofluid in Heat Exchangers using a Buongiorno Model, Applied Mathematics and Computation 254 (2015) 183-203.
[8] W. Duangthongsuk, A.S. Dalkilic, S. Wongwises, Convective heat transfer of Al2O3-water nanofluids in a microchannel heat sink, Curr. Nanosci. 8 (3) (2012)317-322.
[9] J. Li, C. Kleinstreuer, Thermal performance of nanofluid flow in microchannels,Int. J. Heat Fluid Flow 29 (4) (2008) 1221-1232.
[10] J. Li, C. Kleinstreuer, Microfluidics analysis of nanoparticle mixing in a microchannel system, Microfluid. Nanofluid. 6 (2009) 661-668.
[11] R. Saidur, K.Y. Leong, H.A. Mohammad, A review on applications and challenges of nanofluids, Renewable Sustainable Energy Rev. 15 (2011) 1646-1668.
[12] O. Anwar Beg, M.M. Rashidi, M. Akbari, A. Hosseini, Comparative Numerical Study of Single-Phase and Two-Phase Models for Bio-Nanofluid Transport Phenomena, Journal of Mechanics in Medicine and Biology 14 (1) (2014) Article number 14500110.
[13] T. Yousefi, F. Veysi, E. Shojaeizadeh, S. Zinadini, An experimental investigation on the effect of Al2O3-H2O nanofluid on the efficiency of flat-plate solar collectors, Renewable Energy 39 (2012) 293-298.
[14]Tsung-Hsun Tsai, Reiyu Chein, Performance analysis of nanofluid-cooled microchannel heat sinks, International Journal of Heat and Fluid Flow, 28 (2007), 1013-1026.
[15]Mohammad Kalteh, Abbas Abbassi, Majid Saffar-Avval, Arjan Frijns, Anton Darhuber,Jens Harting, Experimental and numerical investigation of nanofluid forced convection inside a wide microchannel heat sink, Applied Thermal Engineering, 36 (2012), 260-268.
[16] Z. Azizi, A. Alamdari , M.R. Malayeri, Convective heat transfer of Cu-water nanofluid in a cylindrical microchannel heat sink, Energy Conversion and Management , 101 (2015), 515-524
[17] , , , Lattice Boltzmann simulation of nanofluid heat transfer enhancement and entropy generation, , 214(2016), 86-95.
[18] , , , , Thermal design exploration of a swirl flow microchannel heat sink for high heat flux applications based on numerical simulations, , 109(2016), 22-34.
[19] , , A comparative analysis of innovative microchannel heat sinks for electronic cooling, , 76(2016), 271-284.
[20] A. Akbarinia, M. Abdolzadeh, R. Laur, Critical investigation of heat transfer enhancement using nanofluids in microchannels with slip and non-slip flow regimes, Applied Thermal Engineering, 31 (2011), 556-565.
[21] ,, , , A study on five different channel shapes using a novel scheme for meshing and a structure of a multi-nozzle microchannel heat sink, , 105(2017), 429-442.
[22] Mohammad Nasiri, Mohammad Mehdi Rashidi,Giulio Lorenzini, Effect of Magnetic Field on Entropy Generation in a Microchannel Heat Sink with Offset Fan Shaped, Entropy 18(2016), 10.
[23] , , Enhanced condensation heat transfer for dielectric fluid within microchannel heat sink, , 106(2017), 518-525.
[24] , , , , , , Numerical and experimental analysis of cooling performance of single-phase array microchannel heat sinks with different pin-fin configurations, , 112(2017), 1547-1556.
[25] Assel Sakanova, Chan Chun Keian, Jiyun Zhao, Performance improvements of microchannel heat sink using wavy channel and nanofluids, International Journal of Heat and Mass Transfer 89 (2015) 59-74.
[26] Ali Radwan, Mahmoud Ahmed, Shinichi Ookawara, Performance enhancement of concentrated photovoltaic systems using a microchannel heat sink with nanofluids, Energy Conversion and Management, 119 (2016), 289-303.
[27] A.S. Tabrizi, H.R. Seyf, Analysis of entropy generation and convective heat transfer of Al2O3 nanofluid flow in a tangential micro heat sink, Int. J. Heat Mass Transfer 55 (2012) 4366-4375.
[28] Lei Chai, Guo Dong Xia, Hua Sheng Wang, Parametric study on thermal and hydraulic characteristics of laminar flow in microchannel heat sink with fan-shaped ribs on sidewalls – Part 1: Heat transfer, , 97(2016), 1069-1080.
[29] Lei Chai, Guo Dong Xia, Hua Sheng Wang, Parametric study on thermal and hydraulic characteristics of laminar flow in microchannel heat sink with fan-shaped ribs on sidewalls – Part 2: Pressure drop, , 97(2016), 1081-1090.
[30] Lei Chai, Guo Dong Xia, Hua Sheng Wang, Parametric study on thermal and hydraulic characteristics of laminar flow in microchannel heat sink with fan-shaped ribs on sidewalls – Part 3: Performance evaluation, , 97(2016), 1091-1101.
[31] Nakatsuka, K.; Jeyadevan, B.; Neveu, S.; Koganezawa, H. The Magnetic Fluid for Heat Transfer Applications. J. Magn. Magn. Mater. 252 (2002), 360-362.
[32] L. Syam Sundar, , , , Effect of full length twisted tape inserts on heat transfer and friction factor enhancement with Fe3O4 magnetic nanofluid inside a plain tube: An experimental study, , 55(2012), 2761-2768.
[33] , , , , , Experimental investigation of forced convection heat transfer and friction factor in a tube with Fe3O4 magnetic nanofluid, , 37(2012), 65-71.
[34] H. Aminfar, M. Mohammadpourfard, Y, Narrimanikahnamouei, A 3D numerical-simulation of mixed convection of a magnetic nanofluid in the presence of non-uniformmagnetic field in a vertical tube using two phase mixture model, J. Magn. Magn. Mater., 323 (2011), , 1963-1972.
[35] H. Aminfar, M. Mohammadpourfard, F.Mohseni, Two-phase mixture model simulation of the
hydro-thermal behavior of an electrical conductive ferrofluid in the presence of magnetic fields. J. Magn Magn. Mater., 324 (2012), 830-842.
[36] H. Aminfar, M. Mohammadpourfard, S. AhangarZonouzi, Numerical study of the ferrofluid flow and heat transfer through a rectangular duct in the presence of a non-uniform transverse magnetic field. J. Magn. Magn. Mater., 327 (2013), 31-42.
[37] F. Garoosi, B. Rohani, M.M. Rashidi, Two-Phase Mixture Modeling of Mixed Convection of Nanofluids in a Square Cavity with Internal and External Heating, Powder Technology 275 (2015) 304-321.
[38] M.M. Rashidi, A. I. S. N. , 35 (7) (2014) 831-848.
[39] M. Akbari, A. Behzadmehr, Developing mixed convection of a nanofluid in a horizontal tube with uniform heat flux. Int. J. Numer. Meth. Heat Fluid Flow, 17 (2007), 566-586.
[40] F. Garoosi, G. Bagheri, M.M. Rashidi, Two phase simulation of natural convection and mixed convection of the nanofluid in a square cavity, Powder Technology 275 (2015) 239-256.
[41] F. Garoosi, B. Rohani, M.M. Rashidi, Two-Phase Mixture Modeling of Mixed Convection of Nanofluids in a Square Cavity with Internal and External Heating, Powder Technology 275 (2015) 304-321.
[42] E.E. Tzirtzilakis, N.G. Kafoussias, Three-dimensional magnetic fluid boundary layer flow over a linearly stretching sheet, Int. Heat Transfer, 132(2010), 11701-11708.
[43] Oztop HF, Abu-Nada E. Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids. Int. J. Heat and Fluid Flow, 29(2008), 1326-1336.
[41] Corcione, M., A semi-empirical model for predicting the effective dynamic viscosity of
nanoparticle suspensions, Heat Transfer Engineering, 33(2012), 575-583.
[44] C.H. Chon, K.D. Kihm, S.P. Lee, S.U.S. Choi, Empirical correlation finding the role of temperature and particle size for nanofluid (Al2O3) thermal conductivity enhancement, Appl. Phys. Lett. 87 (2005) 153107.
[45] Lei Chai, Guodong Xia, Mingzheng Zhou, Jian Li, Numerical simulation of fluid flow and heat transfer in a microchannel heat sink with offset fan-shaped reentrant cavities in sidewall. Int. Comm. Heat and Mass Transfer, 38(2011), 577-584.
[46] J.A. Shercliff, Steady motion of conducting fluids in pipes under transverse magneticfields, Proc. Camb. Philos. Soc. 49 (1953) 136-144.
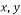 ,z
,z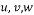
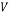
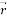
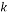
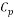
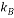
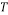
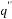
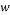
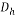
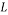
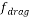
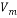
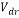
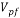
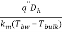
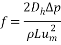
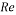 =
=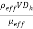
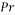
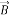
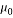
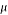
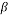
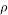
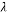
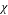
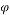
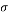
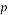
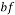
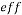
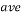
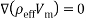
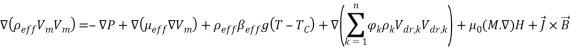
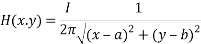
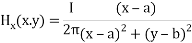
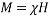
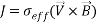
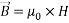
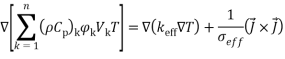
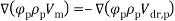
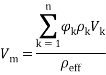
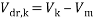
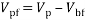
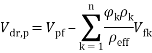
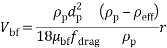
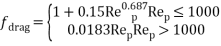
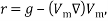
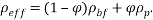
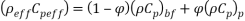

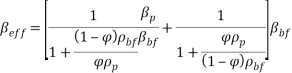
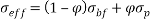 .
.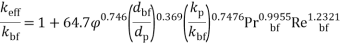
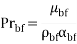
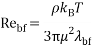
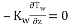 ; u = 0; v = 0 ;P = Patm
; u = 0; v = 0 ;P = Patm