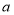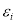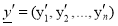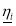Enhancement in Quality and Productivity: a Riskless Approach
Enhancement in Quality and Productivity: a Riskless Approach
by
Vahab Moradinaftchali
Student number: 11225061
to
The School of Mathematical Sciences
in partial fulfillment of the requirements
for the degree of
Doctor of Philosophy
in the subject of
Probability Theory and Mathematical Statistics
in
June, 2016
Dissertation Supervisor
Prof. Lixin Song
Â
Abstract
In today’s industrialized world, the competition for the sale of products is crucial for the survival of the country’s industries. An industry is sustainable and is able to grow and expand that can compete with domestic or foreign counterparts. It is not possible except by raising the quality of manufactured products. Quality in all areas of human life, including the products and services plays an important role. Due to the sensitivity of the industry and its impact on human life, the role of quality in the industrial sector and more precisely in the manufacture of industrial products is stronger and more substantial. The most important effects of quality in manufacturing of industrial products can be summarized as: enhancement in productivity, reduction in costs, market share growth, improvement in business reputation, and satisfaction of both producers and customers.
This study is conducted to show the importance of improvement in quality of the products in profitability as one of the main concerns of the producers is to manufacture their products at the minimum cost and highest customers’ satisfaction. In this study, using quality loss and manufacturing cost functions, a new model for allocation of tolerances of a product’s components simultaneous with selecting quality improvement operations is introduced. Implementation of the improvement operations increases two kinds of costs, i.e. improvement cost and manufacturing cost, whereas decreases quality cost due to reduction in variability of the process.
This research takes advantages of the opposite effect that different cost functions have on each other and the trade-off thereof to develop a cost-effective model in a riskless sense. Therefore, a series of optimization algorithms are presented to select the optimal tolerances simultaneous with improvement operations at the minimum total cost. These algorithms have been designed to considerably save large amounts of computer time by eliminating many redundant evaluations. The results and findings show that the productivity and quality will enhance if both improvement operations and tolerances are chosen properly.
Keywords: Algorithm; Productivity; Optimization; Assembly; Tolerance Allocation
Â
摘   è¦Â
在当今的工业åŒ-ä¸-ç•Œä¸Â,产å“Âéâ€â‚¬Ã¥â€Â®Ã§Å¡â€žÃ§Â«Å¾Ã¤Âºâ€°Ã¥Â¯Â¹Ã¤ÂºÅ½Ã¥â€ºÂ½Ã¥Â®Â¶Ã¤ÂºÂ§Ã¤Â¸Å¡Ã§Å¡â€žÃ§â€Å¸Ã¥Â˜æ˜¯è‡³å…³é‡Âè¦Â的。如果想è¦Â行业稳定å‘展,ä¸Âæ-ÂæˆÂ长和扩大,并ä¸â€Ã¨Æ’½å¤Ÿä¸Žå›½å†…å¤-åŒ行竞争,就è¦Â从æÂÂ高产å“Âè´¨é‡Âæ-¹é¢入手。在人类çâ€Å¸Ã¦Â´Â»Ã§Å¡â€žÃ¥Â„个领域ä¸Â,æ- è®ºæ˜¯äº§å“Â还是æœÂ务,质é‡Â都起ç€关éâ€Â®Ã¦â‚¬Â§Ã¤Â½Å“çâ€Â¨Ã£â‚¬â€šÃ§â€Â±Ã¤ÂºÅ½Ã¥Â·Â¥Ã¤Â¸Å¡Ã¨â€¡ÂªÃ¨ÂºÂ«Ã§Å¡â€žÃ¦â€¢Â感性和对人类çâ€Å¸Ã¦Â´Â»Ã§Å¡â€žÃ¥Â½Â±Ã¥â€œÂ,工业领域ä¸Âçš„è´¨é‡Â更确切地说是工业产å“Âçš„è´¨é‡Â,这一点å˜å¾-越æ¥越é‡Âè¦Â。高质é‡Â的工业产å“Â能够åÂÂ映在以下几点:çâ€Å¸Ã¤ÂºÂ§Ã§Å½â€¡Ã¦ÂÂ高,æˆÂ本é™Â低,市场份é¢Â增长,ä¼Â业声誉上å‡,以åŠçâ€Å¸Ã¤ÂºÂ§Ã¥â€¢â€ 和客户的高满æ„Â度。
该ç â€Ã§Â©Â¶Ã¦-¨åœ¨è¯Â明高质é‡Â产å“Â对ä¼Â业盈利的é‡Âè¦Â性,任何一个产å“Âçâ€Å¸Ã¤ÂºÂ§Ã¥â€¢â€ 都希望以最低的æˆÂ本赢åÂ-最高的客户满æ„Â度。è¿Âçâ€Â¨Ã¨Â´Â¨Ã©â€¡ÂæŸ失和çâ€Å¸Ã¤ÂºÂ§Ã¦Ë†Â本函数是一个全æ-°çš„模å¼Â,çâ€Â¨Ã¤ÂºÅ½Ã¥Ë†â€ é…Â产å“Â组件公差以åŠ选择质é‡Âæâ€Â¹Ã¨Â¿â€ºÃ¦â€œÂ作。æâ€Â¹Ã¨Â¿â€ºÃ¦-¹æ³•çš„实æ-½å¢žåŠ äº†ä¸¤ç§ÂæˆÂ本,å³æâ€Â¹Ã¥-„æˆÂ本和制造æˆÂ本,而质é‡ÂæˆÂ本éšÂçÂۍâ€Å¸Ã¤ÂºÂ§Ã¦Â¥éª¤çš„å‡Â少而é™Â低。
本ç â€Ã§Â©Â¶Ã¥Ë†Â©Ã§â€Â¨Ã¤Â¸ÂåŒæˆÂ本函数é-´çš„相åÂÂ效果与交易,在æ- é£Žé™©çŽ¯å¢ƒä¸Âå¼€å‘一个具有æˆÂ本效益的模型。因æ¤æÂÂ出一系åˆ-的优åŒ-ç®-法æ¥选择最优公差,åÂξ-¶ä»¥æœ€ä½Žçš„总æˆÂ本æÂ¥æâ€Â¹Ã¨Â¿â€ºÃ¦â€œÂ作,这些ç®-法通过消除大é‡Âå†-余的评价已为çâ€ÂµÃ¨â€žâ€˜Ã¨Â®Â¡Ã§Â®-节çœÂ了大é‡Âæ-¶é-´ã€‚ç â€Ã§Â©Â¶Ã§Â»â€œÃ¦Å¾Å“显示,如果æâ€Â¹Ã¨Â¿â€ºÃ¦â€œÂ作和公差选择适当,çâ€Å¸Ã¤ÂºÂ§Ã§Å½â€¡Ã¥â€™Å’è´¨é‡Â都会å¾-到æÂÂ高。
å…³éâ€Â®Ã¨Â¯Â:ç®-法;çâ€Å¸Ã¤ÂºÂ§Ã¥Å ›ï¼›ä¼˜é€‰æ³•ï¼›è£…é…Â;公差分é…Â
Â
CONTENTS
Â
1 Introduction
1.1 Preface
Over time, quality has become a relevant factor in customers’ service research, decision making for customers as well as in services assessment. This phenomenon has gained considerable attention to consumers, investors, industrial organizations, military project or retailers in order to maximized profit and high quality production. Therefore, quality is a key factor to achieve success and better competitive position in business (Feigenbaum[1]). The organizations which use quality as a business strategy and implement effective quality improvement programs will experience good financial returns by time (Rust et al.[2]).
Quality can be defined from multiple points of view, extending from “satisfying customers’ requirements” to “fitness for use” to “conformance to requirements.” It is obvious that any definition of quality ought to incorporate customers, satisfying whom must be the essential objective of any business. Experience during the most recent decades in the U.S. and world markets has plainly exhibited that quality is a standout amongst the most critical components for business achievement and development. Organizations accomplishing higher quality in their products enjoy noteworthy advantage over their competition; hence, it is imperative that the employees in charge of the design, development, and manufacture of products appropriately understand the impressions and procedures used to enhance the quality of products. In this regard, statistical quality control provides the statistical techniques necessary to guarantee and improve the quality of products.
1.2 Historical Evolution in Quality Control
During the last century, most of the statistical quality control techniques that play a fundamental role in statistical process control have been developed. Following provides brief information about the historical evolution in quality control in seven phases:
The first phase covers the time period up to 1900 and is called “Operator Quality Control Period”. The entire product was produced by a small group or a single person, hence, the quality of the item could basically be controlled by an individual who was also the operator, and the volume of production was limited. Since each worker was involved in all stages of a product, a sense of accomplishment was felt which fortifies morale to achieve better products.
The second phase ranged from 1900 to 1920 and is called “Foreman or Supervisor Quality Control Period”. In this period, the concept of mass production based on specialization of labour came with the industrial revolution. An individual was not in charge of the production of the whole item but rather for only a portion of it. The workers who performed similar operations were grouped together under supervision of a manager who undertook the task of guaranteeing that quality was achieved. One disadvantage of this methodology was the abatement in the workers’ feeling of accomplishment and pride in their work.
The third phase (1920-1940) is known as “Inspection Quality Control Period”. Due to growing sophistication in products and processes and increasing volume of production, it became difficult for the foremen to look after all operations. Therefore, the standards were set and the inspectors were designated to check the quality of the products with those standards. In the event of differences between the product and standards, the deficient items were separated for either possible rework or complete rejection. The foundations of statistical parts of quality control were being developed in this interval of time. Using the Shewhart control charts by Walter A. Shewhart in 1924, obtaining the funding of some great organizations such as ASTM, ASME, ASA, and IMS by Walter Shewhart on his efforts to promote statistical quality control (SQC) to industry in 1929, establishment of the work in the areas of acceptance sampling plans by Dodge and Romig in the late 1920s and finding application of such plans in industries in the late 1930s, introducing the Scanlon plan for improvement of the overall quality of work life by J. Scanlon, and the U.S. Food, Drug, and Cosmetic Act of 1938 were important events of this phase.
During the years between 1940 and 1960 the next phase in the evolution process occurred which is known as the “Statistical Quality Control Phase”. A rapid increase in production provisions, acceptance of the principles of sampling plans due to infeasibility of 100% inspection, formation of the American Society for Quality Control (ASQC) which is nowadays known as the American Society for Quality (ASQ), development of the sampling inspection plans for attributes and variables by the military, and development of the Inspection and Quality Control Handbook H107 by the Department of Defense (DOD) are the important events occurred in this period. Moreover, Japanese specialists began to realize the significance of statistical quality control when this new thought was addressed by W. Edwards Deming in 1950. Further impression on the role of management in the achievement of a quality program, which led to a solid responsibility to preparation of a massive program of training and education, was given by J. M. Juran during his visit to Japan in 1954.
The “Total Quality Control” phase occurred during the 1960s. The contribution of several departments and management personnel in the quality control process was an essential achievement of this period. This can also be considered as a change in people’s attitude since the regular thought preceding this time was that the inspection department had the responsibility for quality control.
The sixth phase (1970s) included the contribution of everyone in the company (from the worker to the chief executive officer) and is called the “Total Quality Control Organization-wide Phase”. This concept (the connection of Quality with each person in the company) proceeded in the 1980s as Total Quality System. In this period, Japanese made good use of a graphical tool known as the cause-and-effect diagram. This diagram was first introduced by K. Ishikawa in 1943 and identifies possible causes for an effect or problem. This helps choose appropriate counteraction in the case of a process being out of control. Moreover, the concept of quality improvement was introduced by G. Taguchi in this decade.
The last phase covers the decade 1980s and known as “Total Quality Control System Phase”. In this period, an awareness of the significance of quality was beginning to grow at all levels and the need for the engagement of the quality philosophy to the manufacture of goods and services was recognized after the success of the Japanese industry. Through the Malcolm Baldrige National Quality Award, the importance of quality control and improvement was officially perceived in the United States in 1987. Many standards and guidelines with emphasis on customer satisfaction and continuous quality improvement in the best and most practical and cost-effective ways were developed by different institutions, e.g. ISO, ANSI and ASQ, to support the quality philosophy.
Since 1990 most changes have been in the field of information technology which is the major revolution after the industrial revolution. Progresses in computational technology to solve sophisticated problems for decision making, the use of internet in the areas of online sell and buy, providing online payment and tracking system for customers and etc. are all a digital part of information technology in the twenty first century. Therefore, the present century will keep on encountering a pressure in growth of quality assurance and improvement approaches that can, using innovation and technology, adapt data and analyze them progressively without tolerating errors.
1.3 Improvement of Products Quality
Problems of today and problems of tomorrow are two main problems for the companies that hope to stay in business in order to create constancy of purpose for improvement of product and service. Issues such as maintaining product quality, budgets, sales, profits, employment, adjustment of output so as not to exceed immediate sales, service, public relations, and etc. are factors that are expected to lie in the first group of problems. On the other hand, problems of the future oblige improvement of the company’s competitive position to keep it ongoing and to provide jobs for its employees. It means acceptance of some obligations toward establishment of this purpose such as the followings:
â‘ Innovation: allocation of resources for long-term strategies, e.g. consideration of new service and new product, new skills and materials, method of production, costs of production, marketing and service, training of personnel and supervisors, and satisfaction of the consumer. Innovation is the basis of the future and cannot succeed unless a firm pledge to quality and productivity is established among top managements.
â‘¡ Allocating resources into both research and education.
â‘¢ Continuous improvement of design of product and service as the consumer is the most important part of the production line (Deming[3]).
Therefore, as it is seen, quality has a significant effect to the companies which intend to stay in a long-term business. In order to control the quality of products, the product function variability needs to be controlled. Deviation of a product from its nominal value can occur due to noise factors that are classified in three groups, namely: external factors, manufacturing imperfections and product deterioration. External noise factors also called outer noise or environmental noise and refer to those elements that externally affect the product during its use, such as mechanical or electrical shocks, humidity, temperature, dust, thermal/ electromechanical interference, client abuse, operator’s negligence and so forth. Product deterioration is also known as inner noise and refers to those parameters of product that change due to wear and aging, for example: loss of resilience of springs. Variation from one product to another manufactured under the same specifications is called manufacturing imperfection or between-product noise and or manufacturing variation. This may be due to variation and instability of the elements of the manufacturing, e.g. materials, and processes.
In order to reduce the effects of all these noises so as to produce robust products, Taguchiclassified the counteractions for quality improvement to the three stages, namely offline quality control in R&D, offline quality control in production engineering, and online quality control during production (Taguchi[4]). Further explanation about these stages is given below.
1.3.1 Offline Quality Control in R&D
This stage corresponds to the product design phase and is done in the following three steps:
â‘ System design: This step has an important impact on reduction of manufacturing costs and sensitivity to noise factors. In this step, a prototype design of product will be developed so as to meet the customer needs, and the determination of manufacturing technology, components, parts, assembly system, materials, etc. To meet customer requirements and to decrease the manufacturing costs the best existing technology at the lowest cost will be used here.
â‘¡ Parameter design: A parameter, known as design variable, is a nominal value that needs to be determined to control product’s functional characteristics. Therefore, in this step, the optimum values of design variables will be determined so as to the manufacturing costs and the effect of noise factors are minimized. Furthermore, these values are chosen such that the mean quality of the product is achieved on target.
â‘¢ Tolerance design: The use of low-grade materials and components are inherently assumed during parameter design which would increase tolerances for noise factors. When parameter design fails to achieve proper product’s quality due to quality variation, the tolerance design will be used. As a matter of fact, reduction in tolerances will lead to an increase in manufacturing costs. Therefore, in this step, higher-grade materials or components will be used so as to reduce tolerances while optimizing manufacturing costs.
1.3.2 Offline quality control in production engineering
This stage corresponds to the design of a manufacturing process which will produce products according to the specifications set out in the product design stage. This will be done in three stages as follows:
â‘ System design: The manufacturing process based on costs and related manufacturing technology will be selected in this step.
â‘¡ Parameter design: The main objective of this step is to minimize the impact of the noise factors by purchasing the optimum materials and providing the optimal operating conditions that are determined in the product design stage, for each of the component processes. Reduction in quality variation will enhance process capability and is often done using experimental design.
â‘¢ Tolerance design: Failure in obtaining sufficient tolerances for the process conditions and sources of variability by the parameter design will lead to a use of this step. Tolerance design will then be used to overwhelm quality variation by eliminating such sources so as to obtain the determined quality economically.
1.3.3 Online quality control during production
Briefly, the first two stages respectively optimize either of product design and system design, for reducing the noise factors, in three steps. System design decides the fundamental features of the design such as materials, components, processes, related technology, etc. which will meet the customer needs and some functional and economical requirements. Parameter design minimizes the variation from the target by finding the optimum values of design variables and optimal operating conditions. When parameter design fails to achieve the required level of quality, tolerance design will be used to do so by tightening tolerances cost-effectively. On the other hand, online quality control helps increase robustness after implementing the production line. It can be done by controlling the process parameters, checking quality of the products and in some cases 100 percent product inspection in order to distinguish defectives for recycling or rework. Using such techniques can reduce sensitivity of design to the sources of variability and increase robustness of the products.
It is essential to note that 100 percent inspection to improve product quality means having a plan for defective products. In other words, the manufacturing process is not capable to produce goods according to predefined specifications. In general, the action of inspection to improve the quality is too late and costly. This is because when a product is manufactured any try including inspection, rework, scrap, etc. concerning its quality improvement is too late to be undertaken. It is worth mentioning that there are exceptions and situations that mistakes are unavoidable but unacceptable, and hence, inspection would be necessary to achieve statistical control. The implementation of inspection in production of complicated integrated circuits can be an example of its use at the right time, as it is the only way to separate good items from bad ones. The following points are then perceived:
â‘ Quality, either good or bad, already exists in the manufactured products, and therefore inspection cannot improve quality, nor guarantee it. Quality cannot be inspected into a product as inspection is a late action.
â‘¡ In addition to the high cost and inefficiency of the mass inspection, except in some specific cases, it is not a reliable approach because it cannot properly separate good items from bad ones.
â‘¢ Routine inspection for many reasons such as fatigue, boredom, maintenance of test instruments, etc. is not reliable and therefore inspectors do not reach an agreement among themselves until their effort is brought into statistical control and the number of defectives that they have made is determined.
â‘£ Inspection of small samples of the product enables both the vendor and the customer’s inspectors to investigate about the instruments and tests used to obtain statistical control and to understand each other with a common language.
1.4 Research objectives and notations
1.4.1 Research Objectives
The concept of offline quality control has drawn a great interest from the researchers and practitioners and has been successfully used by many companies and industries since it was first introduced by Taguchi[5]. As mentioned earlier, this stage can be implemented in three phases for controlling noise factors and among them, tolerance design has a particular importance in optimization design and helps allocate optimal tolerances to components so as to minimize the total cost. However, it is worth thinking of more productivity during allocation of the tolerances to the components by taking some improvement operations.
The main motives of using improvement methods can be found in two reasons. First, customers are looking for higher quality products as quality is felt as a need in their life. Second, industries to maintain their competitive position in the market require the use of quality improvement methods to obtain the consent of their clients. It is shown by Shewhart[6], Deming[3] and Rust et al.[2] through some examples based on their studies that productivity does indeed increase as quality improves. However, there are some ambiguities such as: “how much improvement in quality” or “what kind of improvements” that need to be perceived. The question of this research could be “will improvement in quality of some component(s) reduce the total cost more than before?” The current research aims to develop a cost-effective model based on quality improvement, which enables manufacturers to have a robust process with the maximum productivity. In this regard, a riskless approach for allocating the tolerance to a component which results in the minimum total cost by taking improvement operations is first introduced in chapter 3. Through this approach, the fixed relationship between standard deviation and tolerance of the component is first relaxed and then other sources of variability for applying improvement operations are entered into the total cost model. This is because manufacturing cost function only reflects the cost incurred to the producer by tightening the natural tolerance based upon controlling a few sources of variability and not all tangible sources. The model proposed in chapter 3 only considers one component. To develop it for an assembled product with 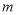 assembly components a riskless approach for taking improvement operations simultaneous with appropriate choices of tolerances which result in the minimum total cost is introduced in chapter 4. Here, the term “riskless” signifies that taking improvement operations should not incur additional costs to the producers. To overcome the difficulties of simultaneous choices of improvement operations and tolerances, a series of algorithms are proposed that help considerably save large amounts of computer time by pruning too many unnecessary evaluations.
assembly components a riskless approach for taking improvement operations simultaneous with appropriate choices of tolerances which result in the minimum total cost is introduced in chapter 4. Here, the term “riskless” signifies that taking improvement operations should not incur additional costs to the producers. To overcome the difficulties of simultaneous choices of improvement operations and tolerances, a series of algorithms are proposed that help considerably save large amounts of computer time by pruning too many unnecessary evaluations.
The highlights of current research are as follows:
â‘ For both a single component and an assembled product, a riskless method is introduced.
â‘¡ A new process capability index is presented.
â‘¢ For simultaneous selection of optimal tolerances and improvement operations a series of algorithms that save large amounts of computer time are proposed.
â‘£ It is shown that productivity may be maximized as a certain amount of quality improvement is applied.
1.4.2 Notations
To enhance readability, the descriptions of the notations are addressed in Table 1-1. Throughout this research, except where otherwise stated, the following notations and symbols will be used as they are described in the second column of Table 1-1.
Table 1-1 Notations
|
notation |
description |
|
|
Number of components |
|
|
index of components |
|
|
index of levels of control |
|
|
index of sources of variability |
|
|
Quality characteristic of component |
|
|
Mean of characteristic |
|
|
Variance of characteristic |
|
|
Quality loss coefficient for component |
|
|
Semi-tolerance of the quality characteristic |
|
|
Lower specification limit |
|
|
Upper specification limit |
|
|
Target |
|
|
Different types of process capability index (PCI) for component |
|
|
Expected quality loss of component |
|
|
Manufacturing cost of component |
|
|
The cost of applying counteractions |
|
|
Fixed costs such as tooling, setup, prior operations and etc. |
|
|
Coefficients of cost-tolerance relationship that depend on the specific machining operations and can be estimated after fitting the data |
|
|
Lower and upper limits of |
|
|
Total cost of component |
|
|
The optimum point for the semi-tolerance of component |
|
|
|
|
|
Variance of the |
|
|
Variance of intangible sources and those sources for which manufacturing cost is calculated |
|
|
Amount of reduction in variability in the |
|
|
The cost corresponding to the reduction in variability in the |
|
|
New process capability index of component |
|
|
New process variability of component |
|
|
The total cost of component |
|
|
Assembly tolerance |
|
|
Tolerance of component |
|
|
Semi- assembly tolerance |
|
|
Arbitrary function which shows the relationship among components |
|
|
The resultant total cost after minimizing the total cost equation |
|
|
The optimum semi-tolerances after minimization |
|
|
Improvement cost of component |
|
|
Net savings of component |
|
|
Maximum value of |
|
|
The number of points chosen from the interval |
|
|
The distance between two consecutive points in the interval |
|
|
The selected level of the |
|
|
Reduction in variance corresponding to the selected level |
|
|
The cost corresponding to the selected level |
|
|
The outputs of the basic algorithm for |
|
|
The improvement cost corresponding to |
|
|
The maximum amount of net savings after applying the first algorithm |
|
|
The total cost corresponding to |
|
|
The improvement cost corresponding to |
|
|
The component corresponding to |
|
|
The maximum amount of net savings after applying the second algorithm |
|
|
The total cost corresponding to |
|
|
The improvement cost corresponding to |
|
|
The component corresponding to |
|
|
The maximum amount of net savings after applying the second algorithm |
|
|
The total cost corresponding to |
|
|
The improvement cost corresponding to |
|
|
The number of algorithms |
|
|
Some arbitrary increment |
|
|
A vector representation of a parent |
|
|
A vector representation of a parent |
|
|
A vector representation of an offspring |
|
|
A vector representation of an offspring |
|
|
Vector of standard deviation |
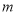
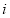
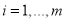
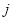
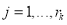
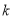

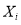
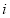
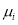


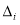
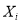 .
.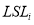
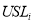
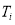
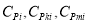


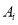
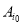

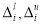
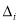
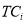
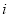 before improvement
before improvement

 mutually independent and normally distributed sources of variability of component
mutually independent and normally distributed sources of variability of component 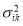
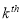 source of variability (
source of variability (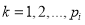 ) of component
) of component 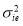

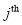 level of control for the
level of control for the 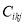
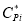

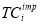
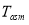


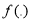
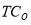


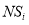
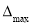
 and
and 
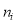
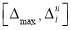

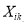
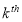 source of variability
source of variability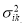
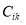
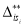
 and some integer
and some integer 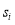

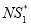
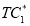
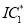

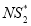
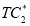
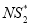 after applying the second algorithm
after applying the second algorithm
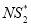 after applying the second algorithm
after applying the second algorithm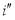
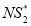
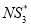
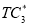
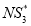 after applying the second algorithm
after applying the second algorithm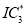
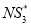 after applying the second algorithm
after applying the second algorithm