Fairness under Transaction Costs
- Introduction
While the Pareto efficiency criterion can be used to rule out inefficient allocations, it allows for very unequal distribution of welfare among the 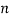 individuals. To the extent that extreme forms of inequality are seen as undesirable, this suggest a need to complement the Pareto efficiency criterion with some welfare distribution criterion. We do this below by introducing fairness in the analysis.
individuals. To the extent that extreme forms of inequality are seen as undesirable, this suggest a need to complement the Pareto efficiency criterion with some welfare distribution criterion. We do this below by introducing fairness in the analysis.
Note that fairness holds under ordinal preferences and does not involve any intertemporal comparison of utility (as envy by the 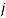 -th consumer is evaluated using her own preferences).
-th consumer is evaluated using her own preferences).
…
- Motivations
We want to answer two related questions: First, when is fairness consistent with Pareto efficiency? And when it is not, what is the welfare cost associated with introducing fairness in economic analysis? To motivate the answers to these questions, this section considers a simple case of an economy composed of two individuals making production and consumption decisions. Having 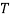 units of total time available, the
units of total time available, the 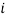 -th individual chooses leisure timeÂ
-th individual chooses leisure time 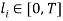 and consumption
and consumption 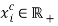 . The
. The 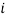 -th individual has preferences represented by the utility function
-th individual has preferences represented by the utility function 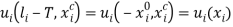 , where
, where 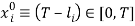 denotes work time, and
denotes work time, and 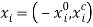 ,
, 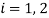 .
.
We first consider situations where there are no transaction costs. Labor times 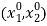 are used in the production of output
are used in the production of output 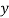 according to the production function
according to the production function 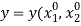 ) satisfying
) satisfying 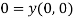 . This allows for heterogeneity in labor/leisure preferences as well as heterogeneity in labor productivity across individuals. The output
. This allows for heterogeneity in labor/leisure preferences as well as heterogeneity in labor productivity across individuals. The output 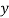 is a consumer good redistributed to the two individuals to satisfy
is a consumer good redistributed to the two individuals to satisfy 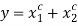 .
.
As discussed in the introduction, fairness is defined as the absence of envy: under fair allocations, no individual prefers someone else’s bundle. In the absence of transaction costs, this implies that 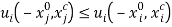 for
for 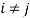 . Note that
. Note that 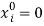 andÂ
and 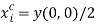 ,
, 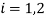 , corresponds to an location that is both feasible and fair (although not efficient). Thus, a fair allocation always exists.
, corresponds to an location that is both feasible and fair (although not efficient). Thus, a fair allocation always exists.
In this section, we illustrate the linkages between fairness and efficiency in the context of a particular example. The example is as follows: Let 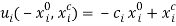 ,
, 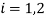 , and
, and 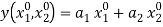 , where the parameters
, where the parameters 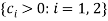 reflect the demand for leisure and the parameters
reflect the demand for leisure and the parameters 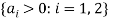 reflect the productivity of labor for the two individuals. Normalizing prices so that the price of
reflect the productivity of labor for the two individuals. Normalizing prices so that the price of 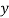 is equal to 1, the shadow cost of time is
is equal to 1, the shadow cost of time is 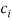 for the
for the 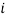 -th individual. In the absence of transaction costs, with
-th individual. In the absence of transaction costs, with 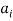 being the marginal value product of labor for the
being the marginal value product of labor for the 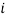 -th individual, the efficient labor supply is
-th individual, the efficient labor supply is 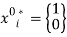 when
when  ,
, 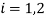 . In this context, an allocation that is both efficient and fair would satisfy:
. In this context, an allocation that is both efficient and fair would satisfy: 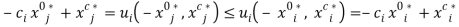 , or
, or 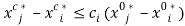 for
for 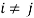 . We consider several scenarios, all illustrated in Figure 1.
. We consider several scenarios, all illustrated in Figure 1.
Scenario S1:  and
and 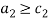 . Under scenario S1, the marginal value product of labor is at least as high as its shadow cost for both individuals. Then, efficient labor is
. Under scenario S1, the marginal value product of labor is at least as high as its shadow cost for both individuals. Then, efficient labor is 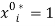 and
and 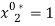 and efficient production is
and efficient production is 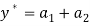 . And under zero transaction costs, an allocation that is both efficient and fair under Scenario S1 satisfies
. And under zero transaction costs, an allocation that is both efficient and fair under Scenario S1 satisfies 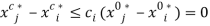 for
for 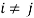 . This implies that
. This implies that 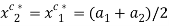 . In this case, there exists a unique allocation that is both fair and efficient: it is the egalitarian allocation where each individual receives the same bundle:
. In this case, there exists a unique allocation that is both fair and efficient: it is the egalitarian allocation where each individual receives the same bundle: 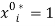 and
and 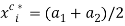 ,
, 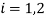 . This allocation generates utilities
. This allocation generates utilities 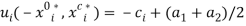 ,
, 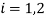 , which is a unique point on the Pareto utility frontier. Figure 1 shows that, under scenario S1, fairness and efficiency can be consistent with each other. Figure 1 illustrates two results. First, under zero transaction costs, fairness excludes many “unfair” allocations located on the Pareto utility frontier. Second, under Scenario S1, fairness can be introduced in the analysis without generating an efficiency loss.
, which is a unique point on the Pareto utility frontier. Figure 1 shows that, under scenario S1, fairness and efficiency can be consistent with each other. Figure 1 illustrates two results. First, under zero transaction costs, fairness excludes many “unfair” allocations located on the Pareto utility frontier. Second, under Scenario S1, fairness can be introduced in the analysis without generating an efficiency loss.
Scenario S2:  and
and 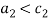 . Under scenario S2, the marginal value product of labor is at least as high as its shadow cost but only for individual 1. Then, efficient labor is
. Under scenario S2, the marginal value product of labor is at least as high as its shadow cost but only for individual 1. Then, efficient labor is 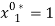 and
and 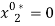 and efficient production is
and efficient production is 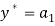 . Under Scenario S2, individual 2 has strong preferences for leisure, implying that it is efficient for this individual to work less (compared to Scenario S1), thus lowering the quantity produced of the good
. Under Scenario S2, individual 2 has strong preferences for leisure, implying that it is efficient for this individual to work less (compared to Scenario S1), thus lowering the quantity produced of the good 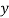 . In the absence of transaction costs, an allocation that is both efficient and fair under Scenario S2 would satisfy
. In the absence of transaction costs, an allocation that is both efficient and fair under Scenario S2 would satisfy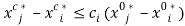 for
for 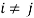 , implying that
, implying that 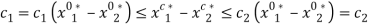 . This inequality can be satisfied only if
. This inequality can be satisfied only if 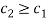 . This generates two possible sub-scenarios: Scenario S2a where
. This generates two possible sub-scenarios: Scenario S2a where 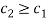 , and Scenario S2b where
, and Scenario S2b where 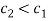 .
.
Under Scenario S2a, 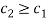 means that individual 2 (who chooses not to work) has a cost of time at least as high as individual 1 (who chooses to work). In this case, there exist allocations that are both fair and efficient. They are the allocations satisfying
means that individual 2 (who chooses not to work) has a cost of time at least as high as individual 1 (who chooses to work). In this case, there exist allocations that are both fair and efficient. They are the allocations satisfying 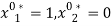 ,
, 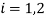 ,
,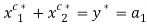 andÂ
and 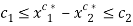 . Given
. Given  , note that this last inequality restricts the difference in consumption
, note that this last inequality restricts the difference in consumption 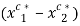 to be positive and bounded between
to be positive and bounded between 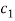 and
and 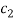 . It means that, under scenario S2a, in the absence of transaction costs and under both fairness and efficiency, individual 1 (who chooses to work) must consume more good
. It means that, under scenario S2a, in the absence of transaction costs and under both fairness and efficiency, individual 1 (who chooses to work) must consume more good 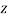 than individual 2 (who chooses not to work). This shows that, being both fair and efficient, the allocations just discussed would correspond to utilities located on the Pareto utility frontier (see Figure 1). Thus, under zero transaction costs, Scenario S2a is an example where fairness can be introduced in the analysis without generating an efficiency loss. In addition, such fair allocations are clearly not egalitarian (as each individual consumes different consumption bundles). Thus, in contrast with Scenario S1, Scenario S2a is an example where egalitarian allocations would not be efficient (see Figure 1).
than individual 2 (who chooses not to work). This shows that, being both fair and efficient, the allocations just discussed would correspond to utilities located on the Pareto utility frontier (see Figure 1). Thus, under zero transaction costs, Scenario S2a is an example where fairness can be introduced in the analysis without generating an efficiency loss. In addition, such fair allocations are clearly not egalitarian (as each individual consumes different consumption bundles). Thus, in contrast with Scenario S1, Scenario S2a is an example where egalitarian allocations would not be efficient (see Figure 1).
Under Scenario S2b, 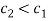 means that individual 2 (who chooses not to work) has a lower cost of time than individual 1 (who chooses to work). In this case, in the absence of transaction costs, fairness and efficiency are inconsistent with each other.[1] Note that this does not imply that fairness cannot be achieved. As noted above, egalitarian allocations exist; and they are always fair. But under Scenario S2b in the absence of transaction costs, such fair allocations cannot be efficient (see Figure 1). In such situations, in contrast with scenarios S1 and S2a, introducing fairness in the analysis cannot be done without generating an efficiency loss. Note that Scenario Sc2 corresponds to
means that individual 2 (who chooses not to work) has a lower cost of time than individual 1 (who chooses to work). In this case, in the absence of transaction costs, fairness and efficiency are inconsistent with each other.[1] Note that this does not imply that fairness cannot be achieved. As noted above, egalitarian allocations exist; and they are always fair. But under Scenario S2b in the absence of transaction costs, such fair allocations cannot be efficient (see Figure 1). In such situations, in contrast with scenarios S1 and S2a, introducing fairness in the analysis cannot be done without generating an efficiency loss. Note that Scenario Sc2 corresponds to 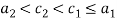 , implying that the individual who has a strong preference for leisure (individual 2) is also less productive (with
, implying that the individual who has a strong preference for leisure (individual 2) is also less productive (with 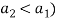 . This shows that the conflict between efficiency and fairness arises from the heterogeneity in both time preferences and productivity across individuals. Under such a scenario, there is necessarily a tradeoff between efficiency and fairness. This raises the question: What is the cost of this tradeoff? We answer this question in section 3 below.
. This shows that the conflict between efficiency and fairness arises from the heterogeneity in both time preferences and productivity across individuals. Under such a scenario, there is necessarily a tradeoff between efficiency and fairness. This raises the question: What is the cost of this tradeoff? We answer this question in section 3 below.
The above analysis was presented in the absence of transaction costs. What happens to the relationships between efficiency and fairness in the presence of transaction costs? To address this issue, we consider the case where labor exchange is costly and distinguish between “actual labor” 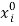 and “effective labor”
and “effective labor” 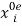 , the difference
, the difference 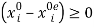 being the amount of labor “wasted” in labor exchange (e.g., due to commuting time). In this context, let
being the amount of labor “wasted” in labor exchange (e.g., due to commuting time). In this context, let 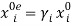 , with
, with 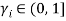 ,
, 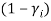 measuring the proportion of labor time wasted by the
measuring the proportion of labor time wasted by the 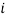 -th individual,
-th individual, 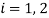 . Then, the production function for
. Then, the production function for 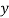 becomes
becomes 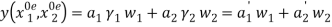 , where
, where 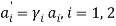 . In this case, transaction costs in the labor market imply a decline in labor productivity, with
. In this case, transaction costs in the labor market imply a decline in labor productivity, with 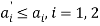 . But note that, conditional on the new parameters
. But note that, conditional on the new parameters 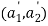 , the analysis of efficiency presented above remains valid.
, the analysis of efficiency presented above remains valid.
Next, consider envy under transaction costs. Let 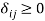 be the cost accrued when the
be the cost accrued when the 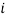 -th individual considers switching place with the
-th individual considers switching place with the 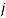 -th individual,
-th individual, 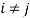 . The switching costs include information cost, relocation cost and retraining cost. Consider the case where prices are normalized such that the price of
. The switching costs include information cost, relocation cost and retraining cost. Consider the case where prices are normalized such that the price of 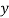 is 1. Then, the absence of envy under transaction costs means that no individual feels that they would be better off switching with others, implying that
is 1. Then, the absence of envy under transaction costs means that no individual feels that they would be better off switching with others, implying that  for all
for all 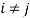 . In the above example, this gives the fairness constraints:
. In the above example, this gives the fairness constraints: 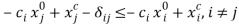 . First, when the transaction costs
. First, when the transaction costs 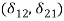 are small (with
are small (with 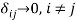 ), then the fairness constraints would generate the results discussed above: fair allocations can be efficient under some situations (i.e., under Scenarios S1 and S2a); but fair allocations are inconsistent with efficiency under other situations (i.e., under Scenario S2b). Second, note the above fairness constraints are always satisfied when the transaction costs
), then the fairness constraints would generate the results discussed above: fair allocations can be efficient under some situations (i.e., under Scenarios S1 and S2a); but fair allocations are inconsistent with efficiency under other situations (i.e., under Scenario S2b). Second, note the above fairness constraints are always satisfied when the transaction costs 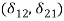 are sufficiently large. Thus, when transaction costs are large, fairness and efficiency would always be consistent with each other. This result holds under any leisure preference parameters
are sufficiently large. Thus, when transaction costs are large, fairness and efficiency would always be consistent with each other. This result holds under any leisure preference parameters 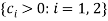 and any labor productivity parameters
and any labor productivity parameters 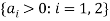 . This shows that the presence of transaction costs can affect fairness in two significant ways: 1/ it increases the odds that any allocation would be seen as fair; and 2/ it makes it easier for efficiency and fairness to be fully consistent with each other. These insights are formally developed in the next section.
. This shows that the presence of transaction costs can affect fairness in two significant ways: 1/ it increases the odds that any allocation would be seen as fair; and 2/ it makes it easier for efficiency and fairness to be fully consistent with each other. These insights are formally developed in the next section.
- Efficiency and Fairness
This section presents an analysis of fairness under general conditions. Going beyond the simple case discussed in section 2, we consider an economy involving 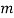 consumer goods and
consumer goods and 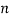 individuals under general preferences and technology. Each individual makes consumption and time allocation decisions. Let
individuals under general preferences and technology. Each individual makes consumption and time allocation decisions. Let 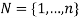 . As in section 2, denote the leisure time of the
. As in section 2, denote the leisure time of the 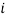 -th individual by
-th individual by 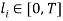 , with corresponding labor time being
, with corresponding labor time being 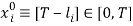 ,
, 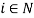 . Denoting consumer goods by
. Denoting consumer goods by 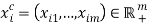 , the
, the 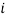 -th individual has preferences represented by the utility function
-th individual has preferences represented by the utility function 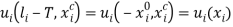 , where
, where 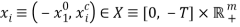 ,
, 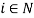 . For welfare analysis, we define a reference bundle
. For welfare analysis, we define a reference bundle 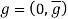 , where
, where 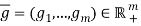 satisfies
satisfies 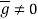 .
.
We make the following assumptions:
As1: The utility function 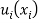 is continuous and quasi-concave on
is continuous and quasi-concave on 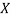 ,
, 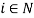 .
.
As2: The function 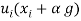 is strictly increasing in
is strictly increasing in 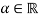 for all
for all 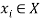 ,
, 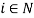 .
.
Assumption As1 is standard in consumer theory. And given 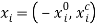 , assumption As2 implies that preferences are non-satiated in the consumer goods
, assumption As2 implies that preferences are non-satiated in the consumer goods 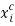 .
.
For the 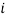 -th individual, define the benefit function
-th individual, define the benefit function
 if
if 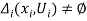 (1)
(1)
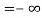 otherwise,
otherwise,
where 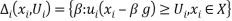 ,
, 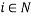 . The benefit function
. The benefit function 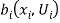 in (1) measures the number of units of the reference bundle
in (1) measures the number of units of the reference bundle  that the
that the 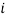 -th individual facing utility
-th individual facing utility  is willing to give up to obtain the bundle
is willing to give up to obtain the bundle 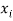 (Luenberger, 1992b). When the reference bundle
(Luenberger, 1992b). When the reference bundle  is chosen such that one unit of
is chosen such that one unit of  is worth
is worth 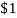 , the benefit function
, the benefit function 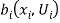 is a monetary welfare measure of willingness-to-pay. Some key properties of the benefit functions will prove useful. First, the benefit function satisfies the translation property
is a monetary welfare measure of willingness-to-pay. Some key properties of the benefit functions will prove useful. First, the benefit function satisfies the translation property 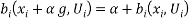 for any
for any 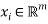 and any finite
and any finite 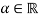 . Second, under As1 (i.e., under the quasi-concavity of
. Second, under As1 (i.e., under the quasi-concavity of 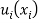 ),
), 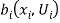 is concave in
is concave in 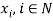 (Luenberger, 1992b, p. 466).
(Luenberger, 1992b, p. 466).
In a production economy, labor is used to produce 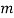 consumer goods. Denote by
consumer goods. Denote by  the
the 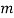 goods produced. Denote labor inputs by
goods produced. Denote labor inputs by 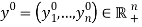 , where
, where 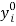 is the quantity of the
is the quantity of the 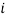 -th individual’s labor used in the production process,
-th individual’s labor used in the production process, 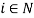 . We use the netput notation (where outputs are positive and labor inputs are negative). Denoting netputs by
. We use the netput notation (where outputs are positive and labor inputs are negative). Denoting netputs by 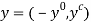 , the production technology is represented by the feasible set be
, the production technology is represented by the feasible set be 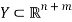 , where
, where  means that outputs
means that outputs 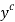 can be produced using labor inputs
can be produced using labor inputs 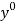 . Note that having
. Note that having 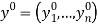 allows for heterogeneity in labor productivity across individuals.
allows for heterogeneity in labor productivity across individuals.
As3: The set 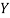 is closed and convex and satisfies
is closed and convex and satisfies 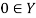 .
.
Next, letting 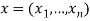 , we define a feasible allocation
, we define a feasible allocation 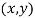 as an allocation which satisfies
as an allocation which satisfies 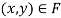 , where
, where 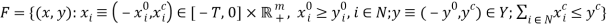 . Accordingly, feasibility requires four conditions: 1/ household decisions are feasible:
. Accordingly, feasibility requires four conditions: 1/ household decisions are feasible: 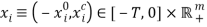 ; 2/ labor use cannot exceed labor supply:
; 2/ labor use cannot exceed labor supply: 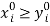 ; 3/ netputs
; 3/ netputs  are feasible as outputs
are feasible as outputs 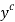 can be produced using labor inputs
can be produced using labor inputs 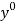 :
:  ; and 4/ aggregate consumption cannot exceed production:
; and 4/ aggregate consumption cannot exceed production: 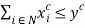 . Let
. Let 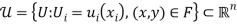 . From As3, note that
. From As3, note that 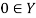 implies that
implies that 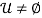 .
.
We start our analysis with the characterization of efficiency. We rely on the standard Pareto efficiency criterion: an allocation 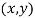 is Pareto efficient if it is feasible and there is no other feasible allocation that can make one individual better off without making someone else worse off. Consider the following optimization problem
is Pareto efficient if it is feasible and there is no other feasible allocation that can make one individual better off without making someone else worse off. Consider the following optimization problem
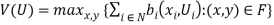 , (2)
, (2)
where 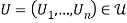 .
.
Definition 1: An allocation 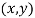 is maximal if it solves equation (2). And it is zero-maximal if, in addition to being maximal, it satisfies
is maximal if it solves equation (2). And it is zero-maximal if, in addition to being maximal, it satisfies 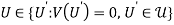 .
.
Zero-maximal allocations are of interest given their close relationship with Pareto optimality. Luenberger (1992a, p. 230-232; 1995, p. 189-192) obtained two key results: 1/ under assumption As2, a Pareto efficient allocation is zero-maximal; and 2/ under assumptions As1-As3, a zero-maximal allocation 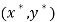 is Pareto efficient with respect to all feasible allocations
is Pareto efficient with respect to all feasible allocations 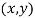 where
where 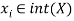 for all
for all . This has several useful implications. First, except for boundary points, a Pareto efficient allocation is equivalent to a zero-maximal allocation. Second, Pareto efficiency corresponds to maximizing aggregate benefit
. This has several useful implications. First, except for boundary points, a Pareto efficient allocation is equivalent to a zero-maximal allocation. Second, Pareto efficiency corresponds to maximizing aggregate benefit 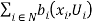 and then redistributing the maximized aggregate benefit
and then redistributing the maximized aggregate benefit 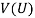 among the
among the 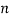 individuals. Third, the set of points
individuals. Third, the set of points 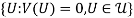 traces out the Pareto utility frontier.
traces out the Pareto utility frontier.
Next, we introduce fairness considerations in the analysis. As motivated in section 2, we explore when are fairness and efficiency consistent with each other. In a way consistent with previous research, we identify fairness as the absence of envy. But we conduct the analysis of fairness allowing for the presence of transaction costs.
Definition 2: An allocation ( is fair if it satisfies
is fair if it satisfies 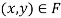 and
and 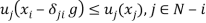 for each
for each 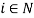 , where
, where 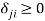 is the number of unit of the reference bundle
is the number of unit of the reference bundle  that would be dissipated by the
that would be dissipated by the 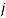 -th individual if the
-th individual if the 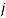 -th individual were to switch place with the
-th individual were to switch place with the 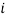 -th individual,
-th individual, 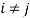 .
.
In our definition of fairness, the condition 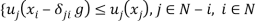 } involves the term (
} involves the term (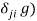 . When the reference bundle
. When the reference bundle  Â is defined such that one unit of
 is defined such that one unit of  is worth
is worth 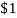 , it follows that
, it follows that 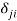 can be interpreted as the cost involved when the
can be interpreted as the cost involved when the 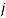 -th individual considers switching place with the
-th individual considers switching place with the 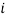 -th individual,
-th individual, 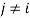 . In this context, the parameters
. In this context, the parameters 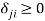 represent transactions costs involved in the fairness evaluation made by individual
represent transactions costs involved in the fairness evaluation made by individual 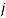 . Note that the absence of switching costs is obtained as a special case when
. Note that the absence of switching costs is obtained as a special case when 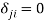 for all
for all 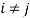 . This the case commonly examined in previous research (e.g., Feldman and Kirman, 1974). But having individuals switching places is expected to be costly: it would typically involve information cost, relocation cost and retraining cost. This suggests that neglecting the transaction costs of switching places is rather unrealistic in fairness analysis.
. This the case commonly examined in previous research (e.g., Feldman and Kirman, 1974). But having individuals switching places is expected to be costly: it would typically involve information cost, relocation cost and retraining cost. This suggests that neglecting the transaction costs of switching places is rather unrealistic in fairness analysis.
In Definition 2, fairness corresponds to the absence of envy under transaction costs. Indeed, the absence of envy means that no individual prefers someone else’s consumption bundle taking into consideration the switching costs 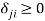 . Letting
. Letting 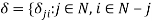 }, define
}, define 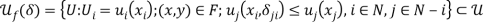 . From assumptions As2 and As3, for any
. From assumptions As2 and As3, for any  , note that
, note that 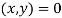 is a feasible as well as a fair allocation. This gives the following result.
is a feasible as well as a fair allocation. This gives the following result.
Lemma 1:Â For any  , a fair allocation always exists:
, a fair allocation always exists: 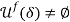 .
.
An allocation 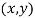 is defined to be fair-efficient if it is fair and there is no other fair allocation that can make one individual better off without making someone else worse off. Letting
is defined to be fair-efficient if it is fair and there is no other fair allocation that can make one individual better off without making someone else worse off. Letting 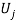 be the utility level obtained by the
be the utility level obtained by the 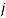 -th individual, note that the fairness conditions (stating the absence of envy)
-th individual, note that the fairness conditions (stating the absence of envy) 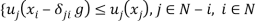 } can be alternatively written as
} can be alternatively written as 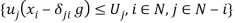 or under assumption As2 as
or under assumption As2 as  . Using the translation property of the benefit function, this last condition can be written as
. Using the translation property of the benefit function, this last condition can be written as  .
.
Next, we consider evaluating fair-efficient allocations by introducing the fairness constraints 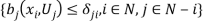 into the optimization problem (2). For given
into the optimization problem (2). For given  and
and  this gives
this gives
 . (3)
. (3)
where 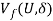 is the maximized aggregate benefit under fairness. Equation (3) indicates that fairness matters when some of the fairness constraints in
is the maximized aggregate benefit under fairness. Equation (3) indicates that fairness matters when some of the fairness constraints in 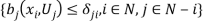 Â are binding in (3).
 are binding in (3).
Definition 3: For a given  , an allocation
, an allocation 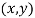 is fair-maximal if it solves equation (3). And it is fair-zero-maximal if, in addition to being fair-maximal, it satisfies
is fair-maximal if it solves equation (3). And it is fair-zero-maximal if, in addition to being fair-maximal, it satisfies  .
.
As discussed in Chavas (2008), there are close relationships between fair-zero maximal allocations and fair-efficient allocations. We say that a consumption bundle 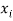 is in the
is in the  -interior of
-interior of 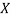 if it satisfies
if it satisfies 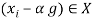 for some
for some 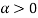 . In the context of equation (3), Chavas (2008, p. 261-262) obtained the following results:
. In the context of equation (3), Chavas (2008, p. 261-262) obtained the following results:
Lemma 2: Given  defined in equation (3),
defined in equation (3),
a/ Under assumption As2, a fair-efficient allocation is fair-zero-maximal.
b/ Under assumptions As1-As3, a fair-zero-maximal allocation 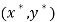 is fair-efficient with respect to all feasible allocations
is fair-efficient with respect to all feasible allocations 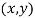 where
where 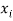 is in the
is in the  -interior of
-interior of 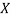 for all
for all .
.
Lemma 2 has several useful implications. First, except for boundary points, a fair-efficient allocation is equivalent to a fair-zero-maximal allocation. Second, a fair-efficient allocation is obtained by maximizing aggregate benefit 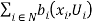 subject to fairness constraints, and then redistributing the maximized aggregate benefit
subject to fairness constraints, and then redistributing the maximized aggregate benefit  among the
among the 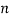 individuals. Third, the set of points
individuals. Third, the set of points 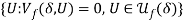 traces out the fair utility frontier (Chavas, 2008).
traces out the fair utility frontier (Chavas, 2008).
Lemma 2 indicates that fair-maximal allocations satisfying (3) can be used to evaluate the efficiency of fair allocations. Two key issues are: Is there and efficiency cost to fairness? And there is, what is it? As written, equation (3) does not identify explicitly the cost of fairness. Next, we proceed to identify the cost of fairness explicitly. For that purpose, considering two individuals 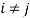 , define the function
, define the function
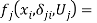
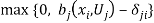 ifÂ
if 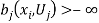 (4)
(4)
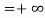 otherwise.
otherwise.
The function 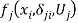 in (4) provides a welfare measure of the cost of envy (net of transaction costs) by the
in (4) provides a welfare measure of the cost of envy (net of transaction costs) by the 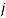 -th individual toward the
-th individual toward the 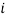 -th individual,
-th individual, 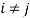 . Indeed, when the benefit function is finite and
. Indeed, when the benefit function is finite and 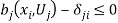 , then the
, then the 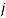 -th individual does not envy the
-th individual does not envy the 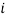 -th individual. In this case,
-th individual. In this case,  in (4) and the associated cost of envy is zero. Alternatively, when
in (4) and the associated cost of envy is zero. Alternatively, when 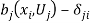 is positive and finite, then
is positive and finite, then 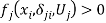 in (4). This corresponds to situations where the
in (4). This corresponds to situations where the 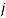 -th individual envies the
-th individual envies the 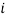 -th individual and thus where the allocation
-th individual and thus where the allocation 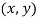 is unfair. The welfare interpretation of
is unfair. The welfare interpretation of 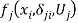 in (4) as the cost of envy (net of transaction costs) follows from
in (4) as the cost of envy (net of transaction costs) follows from  being the number of units of the reference bundle
being the number of units of the reference bundle  the
the 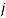 -th individual’s is willing to give up to obtain the bundle
-th individual’s is willing to give up to obtain the bundle 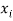 consumed by the
consumed by the 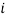 -th individual.
-th individual.
This willingness-to-pay interpretation of 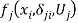 in (4) suggests that there is an alternative characterization of the optimization problem (3). This is stated next (see the proof in the Appendix).
in (4) suggests that there is an alternative characterization of the optimization problem (3). This is stated next (see the proof in the Appendix).
Proposition 1: For a given  and
and 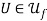 , let
, let 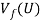 be as defined in equation (3). The maximized aggregate benefit under fairness can be alternatively written as
be as defined in equation (3). The maximized aggregate benefit under fairness can be alternatively written as
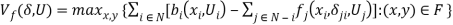 . (5)
. (5)
Proposition 1 states that the equivalence of equation (3) and equation (5) in identifying the maximized aggregate benefit under fairness. But, compared to (3), equation (5) offers a significant advantage: it provides 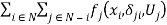 as an explicit measure of the cost of envy. This property will prove to be particularly useful in our investigation (see below).
as an explicit measure of the cost of envy. This property will prove to be particularly useful in our investigation (see below).
From Proposition 1, the results stated in Lemma 2 also apply to the fair-maximal allocations identified in (5). In particular, a fair-maximal allocation is obtained by maximizing aggregate benefit net of envy cost 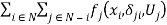 as given in (5). And, except for boundary points, a fair-efficient allocation is a fair-zero-maximal allocation where aggregate net benefit is maximized (yielding
as given in (5). And, except for boundary points, a fair-efficient allocation is a fair-zero-maximal allocation where aggregate net benefit is maximized (yielding 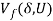 in (5)) and the associated aggregate benefit is entirely redistributed, with
in (5)) and the associated aggregate benefit is entirely redistributed, with  .
.
The term 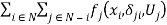 in equation (5) reflects the aggregate cost of unfair allocations. Since
in equation (5) reflects the aggregate cost of unfair allocations. Since  from (4), this aggregate cost is always non-negative. More specially, this aggregate cost is zero under fair allocations (where there is no envy). But
from (4), this aggregate cost is always non-negative. More specially, this aggregate cost is zero under fair allocations (where there is no envy). But 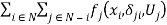 would be strictly positive for allocations
would be strictly positive for allocations 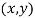 that are unfair. Given
that are unfair. Given 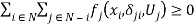 and comparing the maximization problems in (2) and (5) implies the following result.
and comparing the maximization problems in (2) and (5) implies the following result.
Lemma 3: For a given  and
and  ,
,
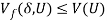 . (6)
. (6)
The inequality in (6) reflects that introducing fairness considerations tends to reduce maximized aggregate benefit. In this context,  provides a general measure of the cost of envy. And in the case where the reference bundle
provides a general measure of the cost of envy. And in the case where the reference bundle  is chosen such that one unit of
is chosen such that one unit of  is worth
is worth 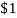 ,
,  is a monetary measure of the cost of envy. In addition, equation (6) implies that the Pareto utility frontier
is a monetary measure of the cost of envy. In addition, equation (6) implies that the Pareto utility frontier 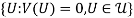 is at least as high as the fair utility frontier
is at least as high as the fair utility frontier 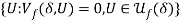 . In other words, introducing fairness in efficiency analysis tends to shift the utility frontier inward. The implications for pricing are explored next.
. In other words, introducing fairness in efficiency analysis tends to shift the utility frontier inward. The implications for pricing are explored next.
- Pricing under Fairness
This section develops a dual approach to efficiency analysis under fairness with the objective of evaluating pricing under fair efficiency. Let  be the set of continuous, non-decreasing functions
be the set of continuous, non-decreasing functions 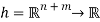 satisfying the translation property
satisfying the translation property  for any
for any 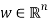 and
and  . Consider the generalized Lagrangian functional
. Consider the generalized Lagrangian functional 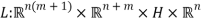
 , (7)
, (7)
where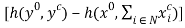 is a penalty function associated with the constraint
is a penalty function associated with the constraint  and
and 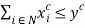 and (5). As discussed below, the functions
and (5). As discussed below, the functions  provide a measure of the value of
provide a measure of the value of  , expressed in number of units of the reference bundle
, expressed in number of units of the reference bundle  . For a given
. For a given 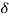 and
and  , consider the optimization problem
, consider the optimization problem
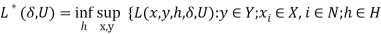 }. (8)
}. (8)
Equation (8) evaluates the saddle-point of the generalized Lagrangian (7). There is close relationship between the fair-maximal allocation given in (5) and problem (8). In general, 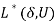 in (8) is an upper bound to
in (8) is an upper bound to 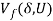 in (5):
in (5): 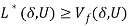 (Bertsekas, 1995; Rubinov et al. 2002). The difference
(Bertsekas, 1995; Rubinov et al. 2002). The difference 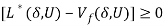 has been called the “duality gap”. Much interest has focused on situations of “zero duality gap” where
has been called the “duality gap”. Much interest has focused on situations of “zero duality gap” where 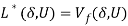 . Under a zero duality gap, the primal problem (5) and the dual problem (8) become equivalent.
. Under a zero duality gap, the primal problem (5) and the dual problem (8) become equivalent.
As4: For a given 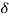 and
and  , the function
, the function 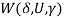 is upper-semi continuous in
is upper-semi continuous in 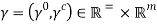 at
at 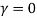 , where
, where
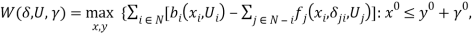
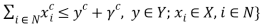
Rubinov et al. (2002) and Chavas and Briec (2012) established that Assumption As4 is a necessary and sufficient condition for a zero-duality gap where 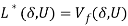 . This generates the following result.
. This generates the following result.
Proposition 2: For a given 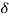 and
and  , and under assumption As4, a fair-maximal allocation satisfies
, and under assumption As4, a fair-maximal allocation satisfies
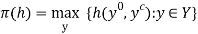 (9)
(9)

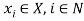 }(10)
}(10)
 .(11)
.(11)
And a fair-zero-maximal allocation satisfies (9), (10 and (11), where 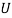 satisfies
satisfies
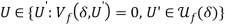 . (12)
. (12)
Equations (9) and (10) follow directly from the maximization problems in (8) with respect to 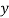 and
and 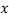 respectively. And the optimization in equation (11) is obtained from the minimization problem with respect to
respectively. And the optimization in equation (11) is obtained from the minimization problem with respect to  in (8). Equation (11) generating the maximized fair benefit
in (8). Equation (11) generating the maximized fair benefit 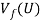 follows from a zero-duality gap under assumption As4. Finally, equation (12) is obtained from the definition of a fair-zero-maximal allocation (in Definition 3).
follows from a zero-duality gap under assumption As4. Finally, equation (12) is obtained from the definition of a fair-zero-maximal allocation (in Definition 3).
The functions  provide a measure of the value of labor
provide a measure of the value of labor 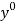 and of the consumer goods
and of the consumer goods 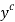 , expressed in number of units of the reference bundle
, expressed in number of units of the reference bundle  . Of special interest is the case where
. Of special interest is the case where  is chosen such that one unit of
is chosen such that one unit of  is worth $1. This amounts to imposing a price normalization rule under which
is worth $1. This amounts to imposing a price normalization rule under which  has a monetary interpretation. Then, the slope of the function
has a monetary interpretation. Then, the slope of the function  provides useful information about pricing for
provides useful information about pricing for 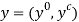 . When
. When  is linear, the slopes of
is linear, the slopes of  with respect to
with respect to 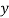 are constant and identify uniform pricing supporting a fair-efficient allocation. But as discussed below, our analysis allows for
are constant and identify uniform pricing supporting a fair-efficient allocation. But as discussed below, our analysis allows for  to be nonlinear, in which case the slopes of
to be nonlinear, in which case the slopes of  are not constant, corresponding to nonlinear pricing.
are not constant, corresponding to nonlinear pricing.
Interpreting 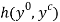 as the value of the netputs
as the value of the netputs 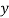 , equation (9) states that, conditional on the pricing scheme
, equation (9) states that, conditional on the pricing scheme  , fair-maximality implies aggregate profit maximization. This is an important result. While profit maximization is a well-known implication of Pareto optimality (e.g., Debreu, 1959), equation (9) shows that introducing fairness considerations in the analysis does not affect the validity of the profit maximization motive. What is new here is that, under fairness, the function
, fair-maximality implies aggregate profit maximization. This is an important result. While profit maximization is a well-known implication of Pareto optimality (e.g., Debreu, 1959), equation (9) shows that introducing fairness considerations in the analysis does not affect the validity of the profit maximization motive. What is new here is that, under fairness, the function  is not restricted to be linear, implying the fair-efficient pricing solution
is not restricted to be linear, implying the fair-efficient pricing solution 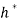 to (11) can involve nonlinear pricing. See below.
to (11) can involve nonlinear pricing. See below.
Similarly, taking 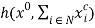 as a measure of value, the function
as a measure of value, the function 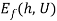 in equation (10) can be interpreted as measuring aggregate consumer expenditure under fairness. To see that, consider the case where
in equation (10) can be interpreted as measuring aggregate consumer expenditure under fairness. To see that, consider the case where  , i.e. where fairness considerations do not play any role. Then, equation (10) would reduce to
, i.e. where fairness considerations do not play any role. Then, equation (10) would reduce to
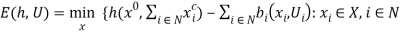 }. (13a)
}. (13a)
Chavas and Briec (2012, p. 685) showed that equation (13a) can be alternatively written as
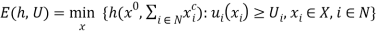 , (13b)
, (13b)
showing that 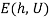 is the minimized aggregate expenditure under the pricing scheme
is the minimized aggregate expenditure under the pricing scheme  and utilities
and utilities 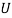 . This has two implications. First,
. This has two implications. First, 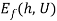 in equation (13) is the minimized aggregate expenditure under fairness, conditional on the pricing scheme
in equation (13) is the minimized aggregate expenditure under fairness, conditional on the pricing scheme  and utilities
and utilities 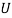 . Second, givenÂ
. Second, given  , comparing (10) and (13) gives the following result.
, comparing (10) and (13) gives the following result.
Lemma 4: For a given  and
and  , and conditional on the pricing scheme
, and conditional on the pricing scheme  , we have
, we have
 . (14)
. (14)
Equation (14) states that aggregate expenditure is as least as large under fair-efficient allocations than under Pareto efficiency. In other words, introducing fairness tends to increase aggregate consumer expenditure.
The solution to equation (11) identifies an optimal pricing scheme 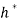 that supports a fair-zero-maximal allocation. fair-efficient allocation. As noted above, the pricing scheme
that supports a fair-zero-maximal allocation. fair-efficient allocation. As noted above, the pricing scheme 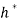 can be nonlinear.
can be nonlinear.
Discuss (12)
- Implications
- Conclusion
This
References
Allais, M., 1943. Traité d’Economie Pure. Imprimerie Nationale, Paris.
Berge, C., 1963. Topological Spaces. Macmillan, New York.
Bhagwati, J., Hudec, R.E. (Eds.), 1996. Fair Trade and Harmonization: Prerequisites for Free Trade? Volume 1. Economic Analysis. MIT Press, Cambridge.
Bolton, G.E. and Katok, E., 1998. An experimental test of the crowding-out hypothesis: the nature of beneficent behavior. Journal of Economic Behavior and Organization 37, 315-331.
Bolton, G.E. and Ockenfels, A., 2000. ERC: a theory of equity, reciprocity and competition. American Economic Review 90, 166-193.
Chaudhuri, A., 1986. Some implications of an intensity measure of envy. Social Choice and Welfare 3, 255-270.
Chavas, J.P. 2008. On Fair Allocations. Journal of Economic Behavior and Organization 68, 258-272
Deaton, A. and Muellbauer, J., 1980. Economics and Consumer Behavior. Cambridge University Press, Cambridge.
Debreu, G., 1959. Theory of Value. Cowles Foundation Monograph. John Wiley and Sons, New York.
Diamantaras, D. and Thomson, W., 1990. A refinement and extension of the no-envy concept. Economics Letters 33, 217-222.
Diewert, W.E., 1974. Applications of duality theory. In: Intriligator, M.D., Kendrick, D.A. (Eds.), Frontiers of Quantitative Economics, II. North Holland, Amsterdam, pp. 106-171, Chapter 3.
Feldman, A. and Kirman, A., 1974. Fairness and envy. American Economic Review 64, 995-1005.
Fehr, E. and Schmidt, K.M., 1999. A theory of fairness, competition and cooperation. Quarterly Journal of Economics 114, 817-868.
Foley, D.K., 1967. Resource allocation in the public sector. Yale Economic Essays 7, 45-98.
Frey, B.S., Oberholzer-Gee, F., 1997. The cost of price incentives: an empirical analysis of motivation crowding-out. American Economic Review 87, 746-755.
Kolm, S.C., 1971. Justice et Egalité. CEPREMAP, Paris.
Konow, J., 2003. Which is the fairest one of all? A positive analysis of justice theories. Journal of Economic Literature 61, 1188-1239.
Luenberger, D.G., 1992a. New optimality principles for economic efficiency and equilibrium. Journal of Optimization Theory and Applications 75, 221-264.
Luenberger, D.G., 1992b. Benefit functions and duality. Journal of Mathematical Economics 21, 461-481.
Luenberger, D.G., 1995. Microeconomic Theory. McGraw-Hill, Inc., New York.
Nishimura, Y., 2003a. Optimal non-linear income taxation for reduction of envy. Journal of Public Economics 87, 363-386.
Nishimura, Y., 2003b. Optimal commodity taxation for reduction of envy. Social Choice and Welfare 21, 501-527.
Pazner, E.A., 1977. Pitfalls in the theory of fairness. Journal of Economic Theory 14, 458-466.
Pazner, E.A. and Schmeidler, D., 1974. A difficulty with the concept of fairness. Review of Economic Studies 41, 441-443.
Rabin, M., 1993. Incorporating fairness into game theory and economics. American Economic Review 83, 1281-1302.
Stiglitz, J.E., 2003. Globalization and its Discontents. W.W. Norton & Co., New York.
Takayama, A., 1985. Mathematical Economics. Cambridge University Press, New York.
Varian, H.R., 1974. Equity, Envy and Efficiency. Journal of Economic Theory 9, 63-91.
Figure 1: Utility Frontiers under Efficiency and Fairness in the Absence of Transaction Cost
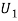





Scenario S1 









Scenario S2a 




 </
</