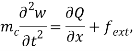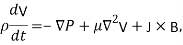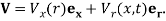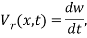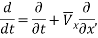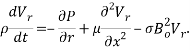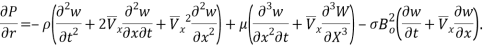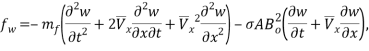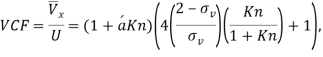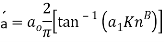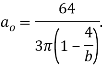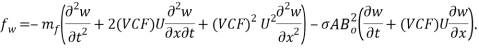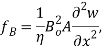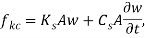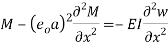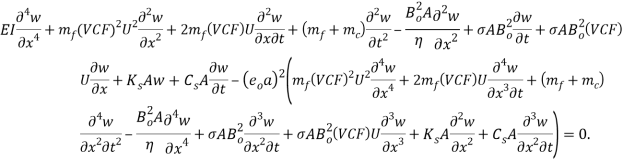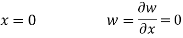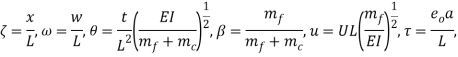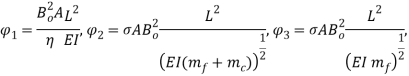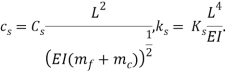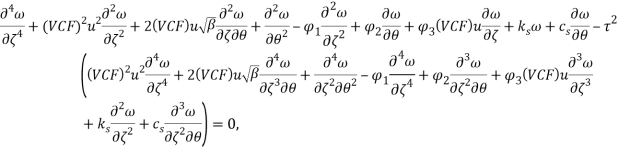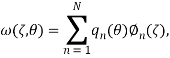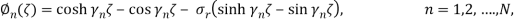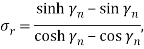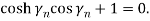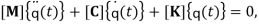Flutter Instability of Cantilevered Carbon Nanotubes
Flutter instability of cantilevered carbon nanotubes caused by magnetic fluid flow subjected to a longitudinal magnetic field
Moslem Sadeghi-Goughari[1], Soo Jeon, Hyock-Ju Kwon
Department of Mechanical and Mechatronics Engineering, University of Waterloo, 200 University Avenue West, Waterloo, Ontario, N2L 3G1, Canada
Abstract:
CNT (Carbon nanotube)-based fluidic systems hold potential for emerging applications such as CNT drug delivery systems for cancer therapy. One of critical issues in designing such systems is to avoid the vibration induced by the fluid flow, which is undesirable and may even promote the structural instability. The main objective of this paper is to investigate the influence of internal magnetic-fluid flow on the fluid structure interaction (FSI) of cantilevered CNTs. The CNT is assumed to be embedded in a biological tissue while conveying a magnetic fluid subjected to a longitudinal magnetic field. For the FSI analysis, we combine the Navier-Stokes theory of magnetic-fluid flow with the Euler-Bernoulli beam model to obtain the governing equations of motion, which is then solved by the extended Galerkin’s method. The size effects of the magnetic fluid and the CNT are considered through small-scale parameters including the Knudsen number (Kn) and the nonlocal parameter. Also, the Kelvin-Voigt model is employed to take into account the viscoelastic behavior of the biological medium. We uncover how the magnetic properties of the fluid flow have an effect on improving the stability of the cantilevered CNT by increasing the flutter velocity.
Keywords: Carbon nanotubes (CNTs); Vibration; magnetic-fluid flow; Small size effects; Fluid structure interaction (FSI).
- Introduction
Discovered by Iijima [1], carbon nanotubes (CNTs) have been recognized as potential nanostructures with unique chemical, electronic, mechanical and magnetic properties [2]. These remarkable properties of CNTs make them attractive in all areas of nanotechnology including nanofluidics and electromagnetics. The hollow cylindrical geometry of CNTs allows them to function as nanopipes for transporting fluid or as nanocontainers for gas storage [3]. In the field of electromagnetics, they have been considered for wide range of applications in nanoelectro-mechanical-systems (NEMS), micro-electro-mechanical-systems (MEMS), nanosensors, spintronics and nanocomposites [4]. In nanomedicine, they hold substantial promise as matrices for compounds simulating neural growth, as biosensors for detection and elimination of cancer cells and as pharmaceutical excipients for creating versatile drug delivery systems [5]. In drug delivery, they can be utilized as nanochannels for delivering drug into target cells guided by a magnetic field [6]. One of important issues in the design of CNT-based fluidic systems is the flow-induced vibration which may promote the structural instability [7].
Vibration of nanotubes conveying fluid has been studied by many researchers. Early works treated the CNT as a simply-supported beam. As one of the first studies in this direction, Yoon et al. [8] investigated the role of internal moving fluid on flow-induced structural instability of CNTs with both ends simply supported. Wang et al. [3] used a multi-elastic beam model to study the vibration and buckling instability of double-wall CNTs (DWCNTs) conveying fluid. Rashidi et al. [9] presented a novel model to investigate the buckling instability of nanotube conveying fluid by considering the small scale effects on the flow field. Lee and Chang [10] used the nonlocal elasticity theory to investigate the small size effect of CNTs on the vibration frequency of the fluid-conveying single-walled CNT (SWCNT). Hosseini and Sadeghi-Goughari [11] developed a nonlocal beam model to study the effect of a longitudinal magnetic field on the structural instability of a SWCNT conveying fluid. Other studies on the flow-induced vibration of simply-supported CNTs include those by Hosseini et al. [12], Mirramazani et al. [13], Khodami Maraghi et al. [14] and Ghobanpour-Arani et al. [15].
In many cases, the CNT-based fluidic systems for drug delivery can be considered as a cantilevered beam. The vibrational behavior of CNT-based fluidic systems with cantilever boundary condition is distinct from those with simply-supported one. Specifically, cantilevered nanotubes conveying fluid may lose their stability by flutter which is a dynamic instability arising from non-conservative systems [16], [17]. Benjamin [18] considered the energy transformation between the flowing fluid and the pipe to study the dynamics of a cantilevered pipe conveying fluid. Gregory and Paidoussis [19] developed a fluid structure interaction (FSI) model to classify the stability conditions of cantilevered pipes conveying fluid. Yu et al. [20] used the transfer matrix method to derive the flutter boundaries of the periodic cantilever pipe conveying fluid. At nanoscales, the small size effects associated with nanostructures and fluid have a crucial impact on the dynamics of nanostructure coupled with fluid flow. Ghorbanpour Arani and Zarei [21] investigated the effect of Knudsen number on eigenvalues of a cantilever CNT conveying nano-magnetic viscous fluid. Bahaadini and Hosseini [22] investigated the effects of nonlocal elasticity and slip condition on the vibrational behavior of viscoelastic cantilever CNTs conveying fluid. Hosseini et al. [23] considered surface effects to study the vibration and instability of a cantilever piezoelectric CNT conveying flowing fluid. Hosseini and Bahaadini [24] investigated the nonlocal flutter instability analysis of CNTs conveying fluid embedded in an elastic foundation under magnetic field.
Although the literature is replete with the studies regarding nanostructures coupled with fluid flow, to the authors’ knowledge, there does not exist any analytical results on the influence of magnetic-fluid flow on the flutter instability of CNTs conveying fluid when they are embedded in a viscoelastic medium.
The main objective of this paper is to investigate the influence of internal magnetic-fluid flow on the flutter stability of a cantilevered CNT which is embedded in a viscoelastic medium and is subjected to a longitudinal magnetic field. To this end, the nonlocal beam theory and the Navier-Stokes equation are coupled to derive the FSI governing equations. The small scale effects of both the fluid flow and the nanotube are taken into account through the Knudsen number (Kn) and the nonlocal parameter. Then, the extended Galerkin’s method is employed to solve the FSI governing equations of motion. Finally, numerical results are presented in graphical form to show the effects of magnetic-fluid flow and small scale parameters on the dynamics of the FSI system.
- Mathematical Modeling
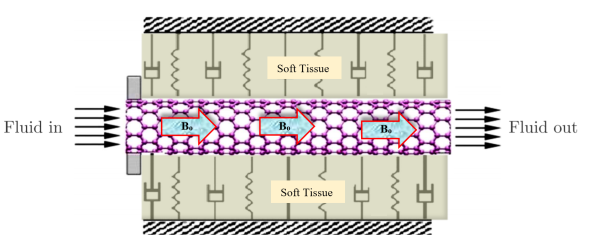
We consider a Newtonian, laminar, incompressible, viscous and magnetic fluid flowing through a cantilever CNT embedded in a biological soft tissue under longitudinal magnetic field (Fig. 1). We can use the Euler-Bernoulli beam theory to model a CNT with a large aspect ratio [25]. The flexural vibration of a CNT, modelled as a single Euler-Bernoulli beam, can be expressed as [13]:
|
|
(1) |
where 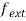 is the external force applied to the CNT in the direction of the flexural displacement,
is the external force applied to the CNT in the direction of the flexural displacement, 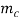 is the nanotube mass per unit length,
is the nanotube mass per unit length, 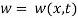 is the flexural displacement of the CNT at the axial coordinate
is the flexural displacement of the CNT at the axial coordinate  and time
and time 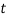 , and
, and 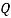 is the resultant shear force acting on the wall cross section, which is equal to the first derivative of the resultant bending moment with respect to
is the resultant shear force acting on the wall cross section, which is equal to the first derivative of the resultant bending moment with respect to 
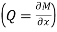 . Here,
. Here, 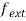 is a combination of several factors acting on the CNT including the forces per unit length induced by the magnetic-fluid flow (
is a combination of several factors acting on the CNT including the forces per unit length induced by the magnetic-fluid flow (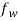 ), by the external longitudinal magnetic field (
), by the external longitudinal magnetic field (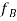 ) and the surrounding biological soft tissue (
) and the surrounding biological soft tissue (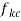 ). Equations for these forces are derived one by one in the following three subsections.
). Equations for these forces are derived one by one in the following three subsections.
- Acting force on CNT due to the magnetic-fluid flow
To incorporate the magnetic-fluid flow to the vibrational equation of the CNT shown in Eq. (1), the momentum-balance equation for the fluid motion is employed. The well-known Navier-Stokes equations for a fluid flow in a magnetic field 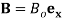 , where
, where 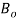 is the magnetic intensity of the longitudinal magnetic field with
is the magnetic intensity of the longitudinal magnetic field with 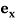 denoting the unit vector along the
denoting the unit vector along the  direction, are stated as follows:
direction, are stated as follows:
|
|
(2) |
where 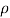 is the fluid density,
is the fluid density, 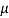 is the dynamic viscosity of fluid,
is the dynamic viscosity of fluid, 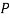 is the fluid pressure and
is the fluid pressure and 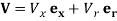 is the fluid velocity in a cylindrical coordinate system with components in the axial (
is the fluid velocity in a cylindrical coordinate system with components in the axial ( ) and the radial (
) and the radial ( ) directions, respectively. The last term is called the Lorentz force that is acting on magnetic-fluid flow from the external magnetic field.
) directions, respectively. The last term is called the Lorentz force that is acting on magnetic-fluid flow from the external magnetic field. 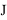 is the electric current density vector given by
is the electric current density vector given by 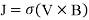 with
with 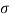 denoting the electrical conductivity of the magnetic fluid.
denoting the electrical conductivity of the magnetic fluid.
To obtain the applied force to the CNT due to the magnetic-fluid flow, the following simplifications are considered:
- Fluid flow is fully developed in the flow direction:
|
|
(3) |
- The slender body theory is applied to the nanotube with high aspect ratio [25]:
|
|
(4) |
|
|
(5) |
where 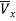 is the average flow velocity in the direction of fluid flow.
is the average flow velocity in the direction of fluid flow.
The force applied to the CNT induced by magnetic-fluid flow is directly related to the fluid pressure gradient in the direction of flexural displacement of the CNT. The Navier-Stokes relation of the flow in  -direction is developed as follows:
-direction is developed as follows:
|
|
(6) |
By substituting Eq. (4) into Eq. (6) and using Eq. (5), the fluid pressure gradient in 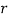 -direction is obtained as:
-direction is obtained as:
|
|
(7) |
The three force terms in the right-hand side of Eq. (7) are associated, respectively, with the fluid inertia, the fluid viscosity and the applied magnetic field. Since the second term is small, it can usually be ignored according to Wang and Ni [25]. Using Eq. (7), we can write down the equation for the forces induced by the magnetic-fluid flow (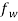 ) as:
) as:
|
|
(8) |
where 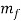 is the fluid mass per unit length and
is the fluid mass per unit length and 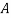 is the cross sectional area of the internal fluid.
is the cross sectional area of the internal fluid.
The flow behavior at nanoscale is substantially different from those at large scales [26]. The small size effects on fluid flow and the low Reynolds number are the most significant differences among all [27]. For the problem at hand, the assumption of no-slip boundary condition between the fluid flow and the CNT’s walls may not hold. Here, we use velocity correction factor (VCF) proposed by Rashidi et al. [9] to consider the slip boundary conditions and the small size effects of fluid flow:
|
|
(9) |
where 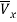 and U are the average flow velocities through nanotube with and without slip boundary conditions, respectively. Kn is Knudsen number defined as the ratio of the mean free path of the fluid molecules to the characteristic length of the flow, which can be used as a discriminating factor to classify fluid flows.
and U are the average flow velocities through nanotube with and without slip boundary conditions, respectively. Kn is Knudsen number defined as the ratio of the mean free path of the fluid molecules to the characteristic length of the flow, which can be used as a discriminating factor to classify fluid flows. 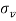 is tangential momentum accommodation coefficient and is considered to be 0.7.
is tangential momentum accommodation coefficient and is considered to be 0.7. 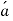 is coefficient and can be defined as a function of
is coefficient and can be defined as a function of 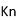 [9]:
[9]:
|
|
(10) |
where 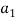 and
and 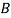 are empirical parameters and are equal to 4 and 0.4, respectively and
are empirical parameters and are equal to 4 and 0.4, respectively and 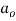 is given by :
is given by :
|
|
(11) |
For the second-order term of slip boundary conditions, 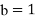 .
.
By Considering the small size effects of fluid flow, the 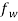 in Eq. (8) can be rewritten as:
in Eq. (8) can be rewritten as:
|
|
(12) |
- Acting force on CNT due to the magnetic field
According to the Maxwell relation, the magnetic force along the direction of the flexural displacement acting on the CNT due to a longitudinal magnetic field can be defined as below:
|
|
(13) |
where 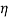 is the permeability of the magnetic field.
is the permeability of the magnetic field.
- Acting force on CNT due to the biological tissue
Pursuant to the viscoelastic properties of biological soft tissues, the CNT is considered to be embedded in a Kelvin-Voigt foundation. So, the applied force to the CNT due to the surrounding viscoelastic material denoted by 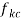 can be expressed as[28]:
can be expressed as[28]:
|
|
(14) |
here, 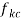 contains two terms. The first one denotes the elastic properties of soft tissue modelled as springs with stiffness
contains two terms. The first one denotes the elastic properties of soft tissue modelled as springs with stiffness 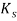 and the second term corresponds to the viscous properties of the tissue simulated by parallel dampers with coefficient
and the second term corresponds to the viscous properties of the tissue simulated by parallel dampers with coefficient 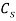 .
.
- Nonlocal modelling of CNT
At nanoscales, the small scale effects of nanostructure have a significant role on the dynamics of systems, and thus necessitate the use of nonlocal theories incorporating small size effects [29]. To this end, we employ the nonlocal elasticity theory to determine the relationship between the resultant bending moment (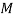 ) and the flexural displacement of the Euler-Bernoulli beam [30]:
) and the flexural displacement of the Euler-Bernoulli beam [30]:
|
|
(15) |
where 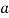 is the internal characteristic length,
is the internal characteristic length, 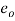 is the material constant, and
is the material constant, and 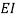 denotes the flexural rigidity of the CNT.
denotes the flexural rigidity of the CNT.
By substituting the terms of external forces (i.e. Eqs. (12-14)), into Eq. (1), and then applying the nonlocal elasticity theory (Eq. (13)), the FSI governing equation of the CNT can be written as:
|
|
(16) |
The corresponding boundary conditions for the cantilevered CNT are
|
|
(17) |
where L is the length of the CNT.
Introducing the following dimensionless variables and parameters:
|
|
(18) |
|
|
|
|
|
Eq. (16) can be rewritten as a dimensionless form:
|
|
(19) |
where 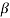 is mass ratio and
is mass ratio and 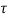 is nonlocal parameter. Here,
is nonlocal parameter. Here, 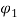 denotes the magnetic force applied to the CNT structure while
denotes the magnetic force applied to the CNT structure while 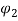 and
and 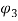 are those applied to the magnetic fluid.
are those applied to the magnetic fluid.
- Galerkin’s method and solution procedure
The main aim of the FSI analysis is to compute the complex-valued eigenvalues of the system, which allow us to determine the vibrational conditions of the CNT. We first use the extended Galerkin method to approximate the partial differential equation in Eq. (19) by a finite dimensional system of coupled ordinary differential equations. Specifically, the flexural displacement of the nanotube can be expressed in a series form as [22]:
|
|
(20) |
where 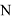 is the number of modes,
is the number of modes, 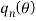 denotes nth modal coordinates and
denotes nth modal coordinates and 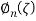 represents the basis function for the nth
represents the basis function for the nth eigenmode.
eigenmode.
For a cantilever nanotube, 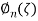 can be written as [22]:
can be written as [22]:
|
|
(21) |
|
|
where the values of 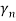 can be derived from the following equation:
can be derived from the following equation:
|
|
(22) |
Applying the extended Galerkin procedure to Eq. (19), a set of coupled ordinary-differential equations is obtained as:
|
|
(23) |
where 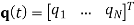 is the overall vector of modal coordinates and the dot notation refers to the time derivative. Also,
is the overall vector of modal coordinates and the dot notation refers to the time derivative. Also, 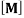 ,
, 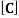 and
and 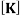 are mass, damping and stiffness matrices of the vibrational system, respectively. Therefore, the dimensionless eigenvalues of nanotube can be calculated numerically from Eq. (23) as a function of
are mass, damping and stiffness matrices of the vibrational system, respectively. Therefore, the dimensionless eigenvalues of nanotube can be calculated numerically from Eq. (23) as a function of 
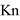 ,
, 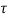 ,
, 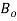 and other parameters of the system.
and other parameters of the system.
- Results and discussion
For the quantitative comparison, we used the same values as those in [9]. Specifically, the nanotube’s aspect ratio, Young’s modulus (ð¸), outer radius (ð‘…ð‘œð‘¢ð‘¡) and thickness (ð‘¡) are set to be 500, 1 TPa, 50 nm and 10 nm, respectively. The magnetic permeability of the CNT (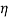 ) is considered to be
) is considered to be 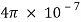 [12]. To make the magnetic effects of fluid more distinctive, we chose the liquid mercury as the fluid medium. The liquid mercury can flow through CNTs when a pressure gradient is applied on the liquid [31]. We assume that the mercury is Newtonian fluid and set the fluid density (
[12]. To make the magnetic effects of fluid more distinctive, we chose the liquid mercury as the fluid medium. The liquid mercury can flow through CNTs when a pressure gradient is applied on the liquid [31]. We assume that the mercury is Newtonian fluid and set the fluid density (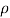 ), electrical conductivity (
), electrical conductivity (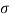 ) to be
) to be 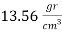 and
and 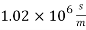 , respectively [32].
, respectively [32].
To characterize the dynamics and instability conditions of the system, the eigenvalue 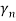 for the nth mode is computed. Generally,
for the nth mode is computed. Generally,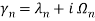 is a complex number and the stability of the system is determined by the imaginary and real components of
is a complex number and the stability of the system is determined by the imaginary and real components of 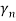 . The complete analysis of the FSI problem involves finding the infinite set of values
. The complete analysis of the FSI problem involves finding the infinite set of values 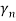 as function of the fluid velocity (
as function of the fluid velocity (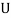 ) and other parameters of the system. As the fluid flow velocity through CNT is increased, the vibration system may become unstable in one or more of its modes. Since the fluid-conveying cantilever CNT is a non-conservative system, it may lose the stability via flutter at its critical flow velocity denoted by
) and other parameters of the system. As the fluid flow velocity through CNT is increased, the vibration system may become unstable in one or more of its modes. Since the fluid-conveying cantilever CNT is a non-conservative system, it may lose the stability via flutter at its critical flow velocity denoted by 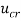 . In the nth mode, for example, the flutter instability may occur when the real part of the nth mode eigenvalue changes its sign from negative to positive and the imaginary component is not zero [22]. It is noted that for the cantilever FSI problem, the flutter fluid speed and corresponding critical eigenvalue is highly dependent on the system’s mass ratio [19].
. In the nth mode, for example, the flutter instability may occur when the real part of the nth mode eigenvalue changes its sign from negative to positive and the imaginary component is not zero [22]. It is noted that for the cantilever FSI problem, the flutter fluid speed and corresponding critical eigenvalue is highly dependent on the system’s mass ratio [19].
- Validation of FSI results
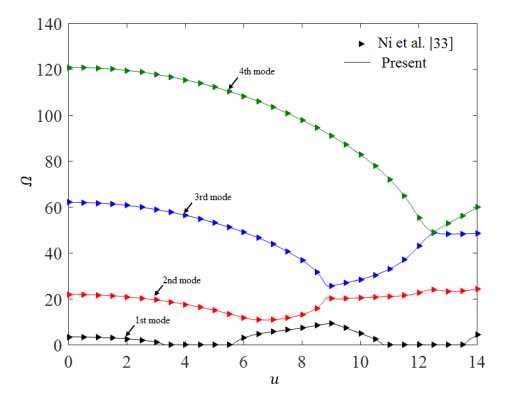
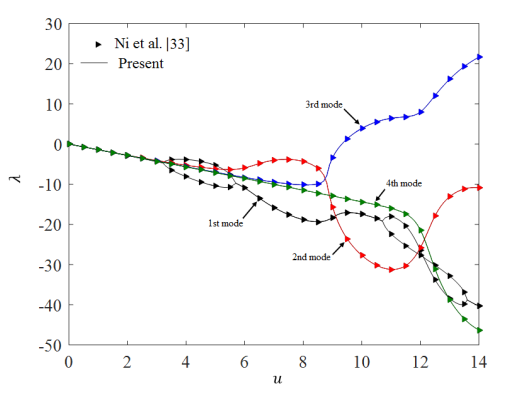
To verify the proposed model derived in section 2, we first examined the four lowest eigen-modes of the system without the effects of magnetic field, surrounding biological medium and small scale parameters. The results are shown in Fig. 2, which coincide with the data published by Ni et al. [33].
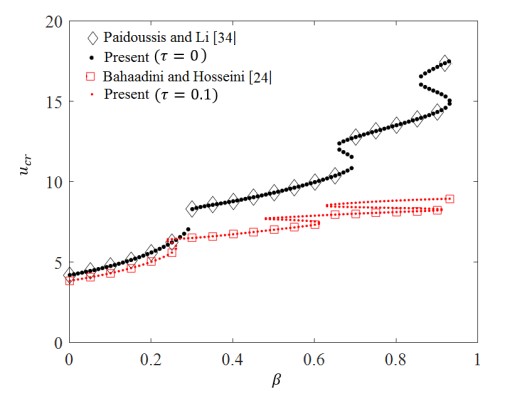
The main purpose of the present work is to characterize the flutter boundaries of the vibrational system as functions of mass ratio in the physically meaningful range of 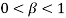 . Fig.3 shows the flutter stability diagrams compared with two existing results. The line with diamond markers compares the data from our model with those published by Païdoussis and Li [34] which demonstrates the case where the small size effects of system is ignored. Similarly, the line with square markers compares our results with those of Bahaadini and Hosseini [24] where the small scale parameters are considered. We can see that our computational results coincide with the existing ones from Refs [23, 33].
. Fig.3 shows the flutter stability diagrams compared with two existing results. The line with diamond markers compares the data from our model with those published by Païdoussis and Li [34] which demonstrates the case where the small size effects of system is ignored. Similarly, the line with square markers compares our results with those of Bahaadini and Hosseini [24] where the small scale parameters are considered. We can see that our computational results coincide with the existing ones from Refs [23, 33].
- Effect of magnetic-fluid flow
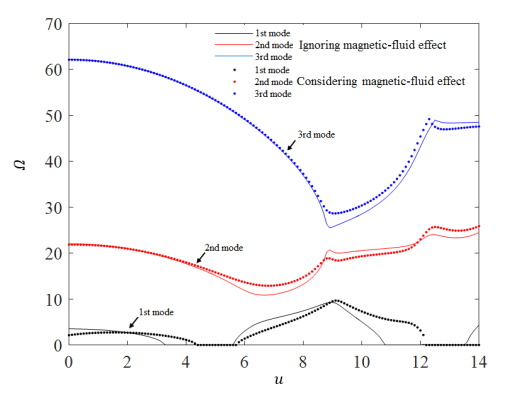
This subsection presents the main results of ours, i.e. the effect of magnetic properties of the fluid flow on the flutter vibration of the system in concern. According to Eq. (19), the magnetic effects occur through three different terms 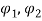 and
and 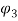 . The first one represents the applied force due to the magnetic properties of the CNT structure and the two other terms are related to magnetic-fluid flow. To focus our attention to understanding the role of magnetic-fluid flow on the structural stability of the system, we investigated the situation where the first term is ignored (i.e.
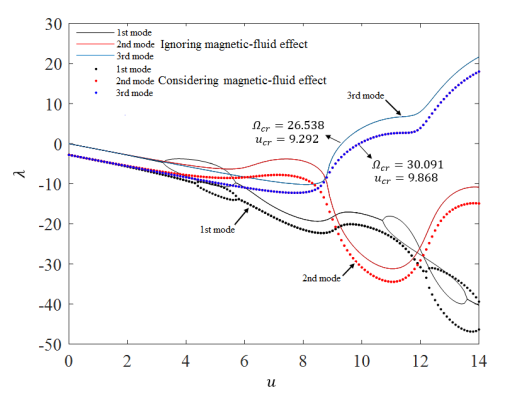
. The first one represents the applied force due to the magnetic properties of the CNT structure and the two other terms are related to magnetic-fluid flow. To focus our attention to understanding the role of magnetic-fluid flow on the structural stability of the system, we investigated the situation where the first term is ignored (i.e. 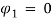 ). Then, the imaginary and real parts of the three lowest dimensionless eigenvalues with and without considering magnetic effects of fluid are computed and presented in Fig 4. As shown in this figure, if we ignore the magnetic fluid flow, the bifurcation of the first eigenvalue
). Then, the imaginary and real parts of the three lowest dimensionless eigenvalues with and without considering magnetic effects of fluid are computed and presented in Fig 4. As shown in this figure, if we ignore the magnetic fluid flow, the bifurcation of the first eigenvalue 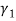 occurs when dimensionless fluid velocity
occurs when dimensionless fluid velocity 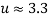 . At this point,
. At this point, 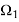 (the imaginary part of
(the imaginary part of 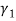 ) becomes zero while the
) becomes zero while the 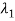 (the real part) splits into two branches. These two branches merge again at the point where
(the real part) splits into two branches. These two branches merge again at the point where 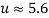 . Therefore, in the range,
. Therefore, in the range, 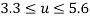 , the system is over-damped and thus remains stable. On the other hand, if we consider the magnetic fluid effect under a high magnetic field (
, the system is over-damped and thus remains stable. On the other hand, if we consider the magnetic fluid effect under a high magnetic field (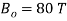 ), the over-damping range changes to
), the over-damping range changes to 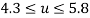 . So, the magnetic properties of fluid flow tend to shift the bifurcation point of first eigenvalue to those with higher fluid velocity and decrease the overdamping region. Also, the eigenvalue diagrams show that, when
. So, the magnetic properties of fluid flow tend to shift the bifurcation point of first eigenvalue to those with higher fluid velocity and decrease the overdamping region. Also, the eigenvalue diagrams show that, when 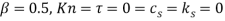 , the system with no magnetic-fluid effects loses its stability by flutter at
, the system with no magnetic-fluid effects loses its stability by flutter at 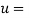 9.292 with the corresponding critical eigenvalue of
9.292 with the corresponding critical eigenvalue of 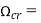 26.539. On the other hand, in the presence of magnetic fluid flow, the flutter instability happens at a higher critical flow velocity
26.539. On the other hand, in the presence of magnetic fluid flow, the flutter instability happens at a higher critical flow velocity 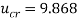 with corresponding critical eigenvalue
with corresponding critical eigenvalue 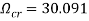 .
.
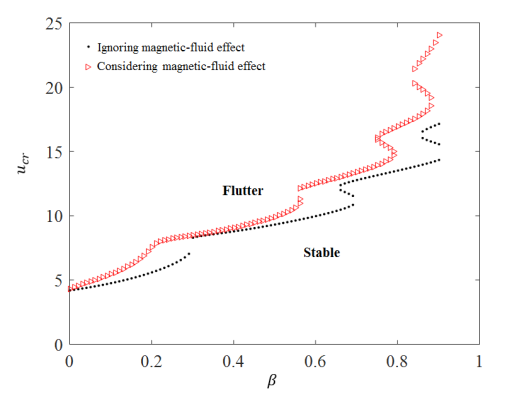
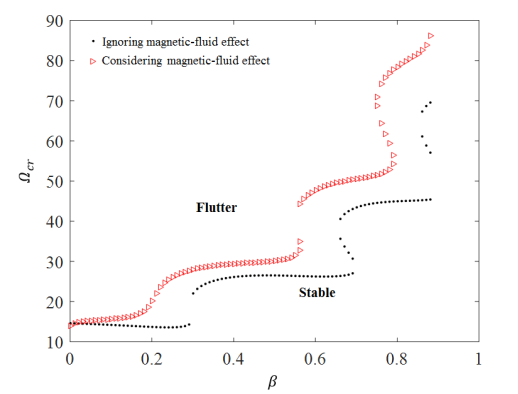
To investigate the magnetic effect on stability in more detail, we computed the critical speed (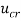 ) and the associated eigenvalue (
) and the associated eigenvalue (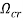 ) for different values of the mass ratio (
) for different values of the mass ratio (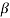 ) and the results are shown in Fig. 5. It is clear from Fig. 5 that the magnetic-fluid flow has an effect of enhancing the vibrational stability of the system by increasing the critical fluid velocity
) and the results are shown in Fig. 5. It is clear from Fig. 5 that the magnetic-fluid flow has an effect of enhancing the vibrational stability of the system by increasing the critical fluid velocity 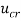 for all range of mass ratio
for all range of mass ratio 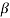 .
.
Note that, the results of this subsection are derived for a high magnetic intensity (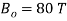 ) to see the effect of magnetic-fluid flow more clearly. To show that this trend remains the same for smaller values of
) to see the effect of magnetic-fluid flow more clearly. To show that this trend remains the same for smaller values of 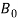 , we computed
, we computed 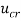 and
and 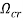 for different values of magnetic field intensity and listed them in Table 1. Clearly, the effect of magnetic field becomes more dominant at high magnetic field and is small for smaller values of
for different values of magnetic field intensity and listed them in Table 1. Clearly, the effect of magnetic field becomes more dominant at high magnetic field and is small for smaller values of 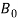 . Nevertheless, it shows the consistent benefits of the magnetic field on enhancing the flutter stability of the system in concern.
. Nevertheless, it shows the consistent benefits of the magnetic field on enhancing the flutter stability of the system in concern.
- Coupled effects of magnetic field with small scale parameters
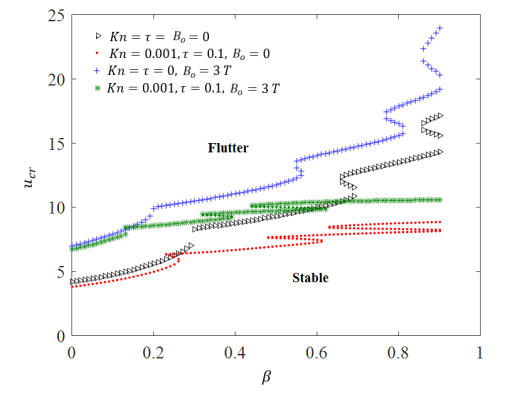
In this subsection, the role of system’s small size effects on the flutter instability of the CNT is investigated. Here, we consider the magnetic effects of CNT structure and fluid flow simultaneously. Since the mean free path of magnetic-fluid flow depends on the fluid temperature, the molecular mean free path and the corresponding Knudsen number of fluid also depends on the fluid temperature. Similarly, the nonlocal parameter of nanostructure can be changed by changing either the internal or the external characteristic length of a CNT. The critical velocity 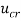 is plotted in Fig. 6 as a function of the mass ratio
is plotted in Fig. 6 as a function of the mass ratio 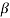 for different small scale parameters when
for different small scale parameters when 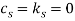 (i.e. in the absence of visco-elasticity). As shown in the figure, the small scale effects of the system tend to decrease the flutter flow velocity for all range of mass ratio, while the stable region is increased in the presence of magnetic field. We can also see that in a certain range of high mass ratio, the magnetic field may amplify the effect of the small scale parameters on the stability of the system. For example, for
(i.e. in the absence of visco-elasticity). As shown in the figure, the small scale effects of the system tend to decrease the flutter flow velocity for all range of mass ratio, while the stable region is increased in the presence of magnetic field. We can also see that in a certain range of high mass ratio, the magnetic field may amplify the effect of the small scale parameters on the stability of the system. For example, for 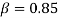 , the small scale effects contributed to decreasing
, the small scale effects contributed to decreasing 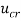 from 13.896 to 8.101 (
from 13.896 to 8.101 (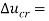 5.795).On the other hand, in the presence of the magnetic field, the small scale effect caused
5.795).On the other hand, in the presence of the magnetic field, the small scale effect caused 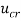 to change from 18.447 to 10.562 (
to change from 18.447 to 10.562 (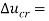 7.885).
7.885).
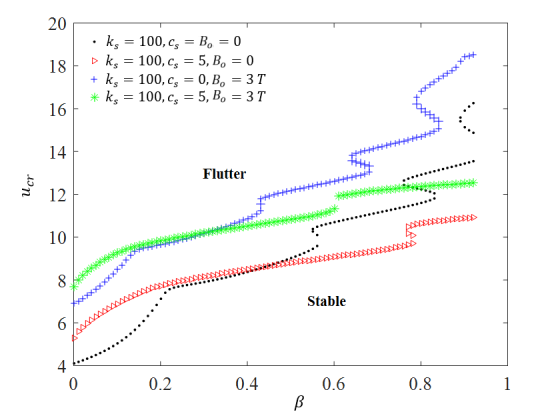
- Coupled effects of magnetic field with viscoelastic parameters
In this subsection, the numerical results of the stability analysis are presented to investigate the coupled effects of the magnetic field and the biological tissue on the vibrational behavior of the system. As we discussed before in section 2, the mechanical characteristics of the biological tissue can be simulated considering it as a viscoelastic material (Kelvin-Voigt foundation). It is obvious that the elastic properties of a soft tissue tend to increase the stiffness of the cantilever system and consequently, will enlarge the stable region [17]. Fig 7 shows the boundaries of the flutter instability as a function of the mass ratio 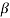 for different values of the damping coefficient (
for different values of the damping coefficient (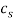 ). In this case, we fixed the stiffness as
). In this case, we fixed the stiffness as 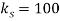 and the small scale parameters as
and the small scale parameters as 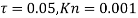 . When we have no magnetic field, for some range of low mass ratio (
. When we have no magnetic field, for some range of low mass ratio (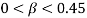 ), the viscous property of the surrounding biological tissue increases the flutter velocity. On the contrary, for
), the viscous property of the surrounding biological tissue increases the flutter velocity. On the contrary, for 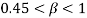 , the viscous property reduces the stable region of the system by decreasing the flutter velocity. The same trend occurs when we have magnetic field; however, the addition of the magnetic field (
, the viscous property reduces the stable region of the system by decreasing the flutter velocity. The same trend occurs when we have magnetic field; however, the addition of the magnetic field (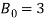 T) has an effect of shifting the critical value of
T) has an effect of shifting the critical value of 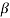 from 0.45 to around 0.32.
from 0.45 to around 0.32.
Conclusion
In this study, the vibration analysis of a CNT conveying magnetic-fluid flow embedded in a viscoelastic medium subjected to a longitudinal magnetic field was investigated. The influence of the magnetic-fluid flow, small size effects of fluid flow and CNT, and the surrounding biological medium on the structural instability of nanotube were considered. It was demonstrated that the magnetic properties of fluid flow had a critical role on the vibrational characteristics of CNTs conveying fluid. Specifically, the magnetic-fluid flow led to shift the bifurcation point of first eigenvalue to those with higher fluid velocity and to decrease the overdamping region. Also, the magnetic effects on the flow field resulted in higher critical flutter velocity, which made the system more stable. This effect was influential on the dynamics of system for high magnetic intensity and it might be ignored at a low intensity magnetic field.
Finally, our results suggested that the stability of system was highly sensitive to the effects of small scale parameters and surrounding biological tissue. We discovered that the small scale effects of system tended to decrease the flutter flow velocity for all range of mass ratio, while in the special range of high mass ratio, the magnetic field might amplify the role of small scale parameters on the stability analysis of system. Besides, we demonstrated that the magnetic properties of system affected the role of biological tissue on the dynamic of CNT.
References
[1]S. Iijima, “Helical microtubules of graphitic carbon,” Nature, vol. 354, no. 6348, pp. 56-58, 1991.
[2]S. C. Fang, W. J. Chang, and Y. H. Wang, “Computation of chirality- and size-dependent surface Young’s moduli for single-walled carbon nanotubes,” Phys. Lett. Sect. A Gen. At. Solid State Phys., vol. 371, no. 5-6, pp. 499-503, 2007.
[3]L. Wang, Q. Ni, and M. Li, “Buckling instability of double-wall carbon nanotubes conveying fluid,” Comput. Mater. Sci., vol. 44, no. 2, pp. 821-825, 2008.
[4]T. Murmu, M. A. McCarthy, and S. Adhikari, “Vibration response of double-walled carbon nanotubes subjected to an externally applied longitudinal magnetic field: A nonlocal elasticity approach,” J. Sound Vib., vol. 331, no. 23, pp. 5069-5086, 2012.
[5]H. Rafii-Tabar, “Computational modelling of thermo-mechanical and transport properties of carbon nanotubes,” Physics Reports, vol. 390, no. 4-5. pp. 235-452, 2004.
[6]W. Zhang, Z. Zhang, and Y. Zhang, “The application of carbon nanotubes in target drug delivery systems for cancer therapies.,” Nanoscale Res. Lett., vol. 6, no. 1, p. 555, 2011.
[7]N. Khosravian and H. Rafii-Tabar, “Computational modelling of a non-viscous fluid flow in a multi-walled carbon nanotube modelled as a Timoshenko beam.,” Nanotechnology, vol. 19, no. 27, p. 275703, 2008.
[8]J. Yoon, C. Q. Ru, and A. Mioduchowski, “Vibration and instability of carbon nanotubes conveying fluid,” Compos. Sci. Technol., vol. 65, no. 9 SPEC. ISS., pp. 1326-1336, 2005.
[9]V. Rashidi, H. R. Mirdamadi, and E. Shirani, “A novel model for vibrations of nanotubes conveying nanoflow,” Comput. Mater. Sci., vol. 51, no. 1, pp. 347-352, 2012.
[10]H. L. Lee and W. J. Chang, “Free transverse vibration of the fluid-conveying single-walled carbon nanotube using nonlocal elastic theory,” J. Appl. Phys., vol. 103, no. 2, 2008.
[11]M. Hosseini and M. Sadeghi-Goughari, “Vibration and instability analysis of nanotubes conveying fluid subjected to a longitudinal magnetic field,” Appl. Math. Model., vol. 40, no. 4, pp. 2560-2576, Feb. 2016.
[12]M. Hosseini, M. Sadeghi-Goughari, S. A. Atashipour, and M. Eftekhari, “Vibration analysis of single-walled carbon nanotubes conveying nanoflow embedded in a viscoelastic medium using modified nonlocal beam model,” Arch. Mech., vol. 66, no. 4, pp. 217-244, 2014.
[13]M. Mirramezani and H. R. Mirdamadi, “Effects of nonlocal elasticity and Knudsen number on fluid-structure interaction in carbon nanotube conveying fluid,” Phys. E Low-Dimensional Syst. Nanostructures, vol. 44, no. 10, pp. 2005-2015, 2012.
[14]Z. Khodami Maraghi, A. Ghorbanpour Arani, R. Kolahchi, S. Amir, and M. R. Bagheri, “Nonlocal vibration and instability of embedded DWBNNT conveying viscose fluid,” Compos. Part B Eng., vol. 45, no. 1, pp. 423-432, 2013.
[15]A. Ghorbanpour Arani, R. Kolahchi, and H. Vossough, “Nonlocal wave propagation in an embedded DWBNNT conveying fluid via strain gradient theory,” Phys. B Condens. Matter, vol. 407, no. 21, pp. 4281-4286, 2012.
[16]M. Hosseini and S. A. FAZELZADEH, “Thermomechanical Stability Analysis of Functionally Graded Thin-Walled Cantilever Pipe With Flowing Fluid Subjected To Axial Load,” Int. J. Struct. Stab. Dyn., vol. 11, no. 3, pp. 513-534, 2011.
[17]M. Hosseini and R. Bahaadini, “Size dependent stability analysis of cantilever micro-pipes conveying fluid based on modified strain gradient theory,” Int. J. Eng. Sci., vol. 101, pp. 1-13, 2016.
[18]T. B. Benjamin, “Dynamics of a System of Articulated Pipes Conveying Fluid. II. Experiments,” Proc. R. Soc. A Math. Phys. Eng. Sci., vol. 261, pp. 487-499, 1961.
[19]R. W. Gregory and M. P. Païdoussis, “Unstable oscillation of tubular cantilevers conveying fluid I . Theory,” Proc. R. Soc. A Math. Phys. Eng. Sci., vol. 293, no. 1435, pp. 512-527, 1966.
[20]D. Yu, M. P. Païdoussis, H. Shen, and L. Wang, “Dynamic Stability of Periodic Pipes Conveying Fluid,” J. Appl. Mech., vol. 81, no. 1, p. 11008, 2013.
[21]A. Ghorbanpour Arani and M. S. Zarei, “Nonlocal vibration of Y-shaped CNT conveying nano-magnetic viscous fluid under magnetic field,” Ain Shams Eng. J., vol. 6, no. 2, pp. 565-575, 2015.
[22]R. Bahaadini and M. Hosseini, “Effects of nonlocal elasticity and slip condition on vibration and stability analysis of viscoelastic cantilever carbon nanotubes conveying fluid,” Comput. Mater. Sci., vol. 114, pp. 151-159, 2016.
[23]M. Hosseini, R. Bahaadini, and B. Jamali, “Nonlocal instability of cantilever piezoelectric carbon nanotubes by considering surface effects subjected to axial flow,” J. Vib. Control, no. December 2015, 2016.
[24]R. Bahaadini and M. Hosseini, “Nonlocal divergence and flutter instability analysis of embedded fluid-conveying carbon nanotube under magnetic field,” Microfluid. Nanofluidics, vol. 20, no. 7, pp. 1-14, 2016.
[25]L. Wang and Q. Ni, “A reappraisal of the computational modelling of carbon nanotubes conveying viscous fluid,” Mech. Res. Commun., vol. 36, no. 7, pp. 833-837, 2009.
[26]C.-M. Ho, “Microflows and Nanoflows Fundamentals and Simulation,” Physical Review E, vol. 67, no. 4. pp. 255-309, 2004.
[27]M. Sadeghi-Goughari and M. Hosseini, “The effects of non-uniform flow velocity on vibrations of single-walled carbon nanotube conveying fluid,” J. Mech. Sci. Technol., vol. 29, no. 2, pp. 723-732, 2015.
[28]P. Soltani, M. M. Taherian, and A. Farshidianfar, “Vibration and instability of a viscous-fluid-conveying single-walled carbon nanotube embedded in a visco-elastic medium,” J. Phys. D. Appl. Phys., vol. 43, no. 42, p. 425401, 2010.
[29]L. Wang, “Vibration and instability analysis of tubular nano- and micro-beams conveying fluid using nonlocal elastic theory,” Phys. E Low-Dimensional Syst. Nanostructures, vol. 41, no. 10, pp. 1835-1840, 2009.
[30]J. N. Reddy and S. D. Pang, “Nonlocal continuum theories of beams for the analysis of carbon nanotubes,” J. Appl. Phys., vol. 103, no. 2, 2008.
[31]Z. Q. Zhang, H. W. Zhang, Y. G. Zheng, J. B. Wang, and L. Wang, “Transport of liquid mercury under pressure in double-walled carbon nanotubes,” Curr. Appl. Phys., vol. 8, no. 2, pp. 217-221, 2008.
[32]C. K. Chiang et al., “Electrical conductivity in doped polyacetylene,” Phys. Rev. Lett., vol. 39, no. 17, pp. 1098-1101, 1977.
[33]Q. Ni, Z. L. Zhang, and L. Wang, “Application of the differential transformation method to vibration analysis of pipes conveying fluid,” Appl. Math. Comput., vol. 217, no. 16, pp. 7028-7038, 2011.
[34]M. P. Paı̈doussis and G. X. Li, “Pipes Conveying Fluid: A Model Dynamical Problem,” Journal of Fluids and Structures, vol. 7, no. 2. pp. 137-204, 1993.
List of Tables
Table 1. Critical values of dimensionless flutter flow velocity and corresponding eigenvalue for different values of the magnetic field intensity (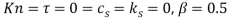 ).
).
|
|
0 |
5 |
10 |
20 |
40 |
80 |
|
|
9.292 |
9.294 |
9.299 |
9.320 |
9.409 |
9.868 |
|
|
26.538 |
26.552 |
26.595 |
26.7623 |
27.417 |
30.091 |
List of Figures.
|
|
Fig. 1. Configuration of CNT conveying magnetic fluid embedded in biological tissue subjected to a longitudinal magnetic field.
|
(a) |
|
|
(b) |
|
Fig. 2. Validation of the four first eigenvalues of cantilever system (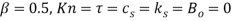 ), (a) imaginary part and (b) real part.
), (a) imaginary part and (b) real part.
|
|
Fig. 3. Validation of the flutter instability boundary of cantilever system for (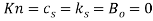 ).
).
|
(a) |
|
|
(b) |
|
Fig. 4. Magnetic-fluid effect in (a) Imaginary and (b) real parts of the lowest three modes eigenvalues for high magnetic field (ðµð‘œ = 80 𑇠) and for (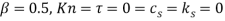 ).
).
|
(a) |
|
|
(b) |
|
Fig. 5. Influence of magnetic-fluid properties on the stability boundaries, as a function of mass ratio 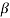 for high magnetic field (ðµð‘œ = 80) and for (
for high magnetic field (ðµð‘œ = 80) and for (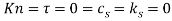 ): (a) dimensionless flutter speed, and (b) dimensionless flutter eigenvalue.
): (a) dimensionless flutter speed, and (b) dimensionless flutter eigenvalue.
|
|
Fig. 6. The coupled effects of the magnetic field with small scale parameters on the critical speed, as a function of non-dimensional mass ratio 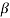 (
(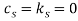 ):
):
|
|
Fig. 7. The coupled effects of the magnetic field and viscoelastic parameters on the critical speed, as a function of the non-dimensional mass ratio 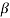 (
(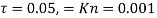 ):
):