Fuzzy Logic Based Smart Solar Power MPPT
Design and Optimization of a Fuzzy Logic Based Smart Solar Power Maximum Power Point Tracker
A. KocabaÅŸ and H.Ä°. OkumuÅŸ
Karadeniz Technical University, Trabzon/Turkey
Abstract- As the issue of efficiency is one of the most important fundamentals of solar power generation, maximum power point tracking (MPPT) systems have an important duty in solar power management systems in solar power generation. This paper includes study of the design and improvement of fuzzy logic based solar power MPPT, and the methodology to achieve the best system performance. MPPT system was evaluated at the DC-DC power converters’ ability of impedance conversion point of view and cooperation of fuzzy logic theory. The parameters of fuzzy inference system are optimized to obtain the fastest and accurate system responses. The performance of the proposed fuzzy logic based MPPT under various operating conditions compared and improvement of this performance is dealt with. The fuzzy logic MPPT function realized using a buck-boost power converter. Computer simulations practiced and simulation results also represented.
Keywords- Maximum Power Point Tracking, Fuzzy Logic Control, Solar Power Generation.
Solar power is one of the most harmless and cleanest, plentiful supply of energy in the world. It is unfailing and like to be our fundamental supply of power in future [1]-[2]. Solar power has already used widely for industrial, commercial, residential and military applications. Performance of solar power generation by photovoltaic (PV) cells depends on the environmental conditions such as insolation, sunlight tilt, load variations, airmass and cell temperature [10]. Power converter units should be associated with the PV cells and the load to control the power flow from the PV cells to the load. PV systems use MPPT systems to maximize power output, by the ability of continually arranging the duty ratio increment command of the switching device in the power converter unit. Algorithms used in MPPT systems maximize power extractions of PV cells by controlling the duty ratio of the power converter with the changing PV cell output variable combinations like changes in power versus changes in voltage etc. MPPT algorithms such as perturb and observe, incremental conductance have been evaluated until now. [3]. Unchanging step size for the control signal, increment of the duty ratio command, used in these methods. Too small steps sizes cause slow tracking process and too large step sizes cause oscillations around the maximum power point (MPP).
To perform automatically adjusting step sizes, variable step sizing algorithms such as fuzzy logic has been developed [4]-[7]. Specification of fuzzy logic controllers is made according to their skill of simulating human thinking. Different than conventional controllers, fuzzy controllers have the ability to experimental methods and their results to design variable step sizes of control signals without the need of understanding the system’s mathematical model [9]. Effectiveness of the MPPT algorithm is directly related with the input and the output variables that are selected for the system. In general for output variable, duty ratio of the power switch selected. As input variables; power (P) versus voltage (V) slope and changes of the slope, P-V slope and variation of power, variation of power and variation of voltage, sum of conductance and increment of conductance would be selected [8]. In this paper as inputs of the controller variation of power and variation of voltage, as an output duty ratio of the power switch selected.
Sunpower SPR-305E-WHT-D (One series module and one parallel strings) PV panel used for simulations in this paper. The characteristics of the PV panel at 25 °C and at various irradiation levels are shown in Figure 1. The characteristics of the PV panel at 1000 W/m2 and at various temperature levels are shown in Figure 2. To make the analysis simple, we have worked on resistive load. Figure 3 illustrates the circuitry of PV panel and resistive load, and current (I)-voltage (V) characteristics with an irradiation 1000 W/m2 and temperature of 25 °C. The intersection of the I-V characteristic curve (blue) of the PV panel and load I-V curve (red) is the operating point of the system. From this figure it can be observed that the operating point changes with the change of the load value. The maximum power point (MPP) can be achieved through proper selection of the load. Maximum power may be extracted from the PV array by incorporating an intelligent mechanism altering the load resistance of the PV array. Power converters are usually used to achieve this purpose.
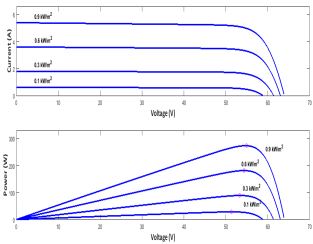Figure 1. The characteristics of the PV panel at 25 °C and at various irradiation levels.
Figure 2. The characteristics of the PV panel at 1000 W/m2 and at various temperature levels.
Figure 3. PV system with resistive load
Figure 4 shows the block diagram of the investigated MPPT system. The system includes a PV panel, a buck-boost power converter and a fuzzy logic based MPPT controller. The function of controlling power flow from source to the load is carried out by the zeta type buck-boost converter as shown in Figure 5. The values of converter circuit elements are Lin = 11 µH, L1 = 378 µH, CIN = C1 = 1000 µF and CPV = 680 µF. The pulse width modulation (PWM) switching frequency was set to 200 kHz. Internal resistances were ignored to obtain (1) on the converter’s input and output voltage equation in steady state:
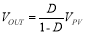(1)
If we assume that converter operates lossless with a resistive load RL, the value of the power obtained from this PV system would be:
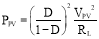(2)
It is demonstrated additionally, in Figure 5, that P-V curves at miscellaneous irradiation levels according (2) and miscellaneous duty ratio commands with the ohmic load 3 Ω. The intersections show the operating points of PV system.
In this study fuzzy theory is used to design the MPPT controller. Required fuzzy input variables are generated by fuzzy MPPT controllers by reading voltage and current signals obtained from the PV panel. The fuzzy input variables would then can be used to calculate the increment of the duty ratio command for adjusting operating point of the PV panel in order to maximize the power extraction. In Figure 6 the flowchart of the calculation process illustrated. Designs of fuzzy controllers are varies according to the input variables selected. As mentioned before in this paper as input variables, variation of power and variation of voltage of the PV array selected.
Figure 4. Solar MPPT system.
Figure 5. Power converter and PV power characteristics.
Figure 6. Flowchart of calculation process.
A. Fuzzy MPPT Tracking Algorithm
In this study fuzzy logic MPPT system used variations of PV cell power output (∆PPV) and variations of voltage (∆VPV) as the fuzzy input variables. By using MATLAB Simulink proposed solar power maximum power point tracking system implemented and universe of discourse (UOC) of input and output membership functions determined. After determination of UOD membership functions, they are grouped with the names negative big, negative small, zero, positive small, positive big (NB, NS, ZE, PS, PB). Fuzzy rules database is shown in Figure 7. Iterations made by moving on the P-V slope’s specified regions as shown in the figure 7.
Figure 7. Fuzzy rules for algorithm using ∆PPV and ∆VPV as the inputs.
First of all symmetric membership functions used in the simulations as shown in Figure 9 and then asymmetrical membership functions used as shown in Figure 10. The performance difference compared then. For fuzzification; Mamdani method and for defuzzification; centre of gravity method used in this study. Fuzzy interface system evaluated by using MATLAB Simulink fuzzy logic toolbox.
Figure 8. Fuzzy controller’ s surface of rule base.
Figure 9. (a) Membership function for ∆PPV (b) Membership function for ∆VPV (c) Membership function for increment of duty ratio command.
Figure 10. Asymmetrical input membership functions (a) Membership function for ∆PPV (b) Membership function for ∆VPV (c) Membership function for increment of duty ratio command.
Purposed MPPT system is simulated by using different types of membership functions for comparison and validation. MATLAB/Simulink model block diagram of the system is shown in Figure 11.
Figure 11. MATLAB/Simulink model block diagram of the system
By using membership functions shown in Figure 9 the simulation results obtained as shown in Figure 12 and by using membership functions shown in Figure 10 the simulation results obtained as shown in Figure 13.
Figure 12. Simulation results (symmetrical membership functions used)
Figure 13. Simulation results (asymmetrical membership functions used)
As shown in figures above when symmetrical membership functions used the fuzzy controlling system was unable to respond quickly to the rapid changes of irradiation so that fitting time of output power curve was longer and this is a disadvantage of the controlling system that is undesired. Beside at low irradiance levels MPPT controller couldn’t produce accurate control signals and PV panel’s operating point was different than the maximum power point.
The performance difference of the designed system when two types of membership functions used respectively can be seen more clearly from Figure 14.
Figure 14. Output power of PV panel.
Here we can see the disadvantages of using symmetrical membership functions. To overcome this problem and improve the system response speed to the changes of irradiation then asymmetrical membership functions has developed. Another benefit of developed system is that, at low irradiation levels precision of MPPT is more higher.
In this paper a fuzzy logic based solar maximum power point tracking system was designed and different types of membership functions were used to optimize system power generation performance. To achieve the goal of higher precision and fastest system responses to the changes of irradiation levels different types of membership functions of inputs of fuzzy inference system were researched and compared with each other. It was revealed that using asymmetrical membership functions in the fuzzy logic controller had improved system performance at all operating conditions. From the results of simulations it can be inferred that the system performance is directly related with the optimization of the membership functions of fuzzy inference system. This study also leads to the study of the designing methodology of optimization of asymmetrical membership functions for better system performance.
References
[1] International Energy Agency. Technology Roadmap: Solar Photovoltaic Energy, IEA Publications: Paris, France, 2014.
[2] K. Tomabechi, Energy Resources in the Future. Energies 2010, pp. 686-695
[3]N. Femia, G. Petrone, G. Spagnuolo, M. Vitellio, “Optimization of Perturb and Observe Maximum Power Point Tracking Method.” IEEE Trans. Power Electron. 2005, pp. 963-973.
[4]T. Yong, B. Xia, Z. Xu, W. Sun, Modified Asymmetrical Variable Step Size Incremental Conductance Maximum Power Point Tracking Method for Photovoltaic Systems. J. Power Electron. 2014, pp. 156-164.
[5]C.S. Chin, P. Neelakantan, H.P. Yoong, K.T.K. Teo, “Optimisation of Fuzzy Based Maximum Power Point Tracking in PV System for Rapidly Changing Solar Irradiance.” Trans. Sol. Energy Plan. 2011, pp. 130-137
[6]T. Radjai, P.J. Gaubert, L. Rahmani, “The new FLC-Variable Incremental Conductance MPPT Direct Control Method Using Cuk Converter.” In Proceedings of the 2014 IEEE 23rd International Symposium on Industrial Electronics (IEIE), Istanbul, 2014, pp. 2508-2513.
[7]R. Rahmani, M. Seyedmahmoudian, S. Mekhilef, R. Yusof, “Implementation of Fuzzy Logic Maximum Power Point Tracking Controller for Photovoltaic System.” 2013, pp.209-218.
[8]J-K. Shiau, Y-C. Wei, B-C. C, “A Study on the Fuzzy Logic Based Solar Power MPPT Algorithms Using Different Fuzzy Input Variables.” ISSN 1999-4893, 2015.
[9]T.J. Ross, “Fuzzy Logic With Engineering Applications”, vol 2, pp. 1-652.
[10]R. Hernanz, C. Martin, Z. Belver, L. Leseka, Z. Guerrero, P. Perez, ” Modelling of Photovoltaic Module.”, International Conference on Renewable Energies and Power Quality, 2010.