How Competition affects Social Preferences

Does competition affect social preferences in the context of a bargaining game?

Abstract

In the first part of this paper, we have a generally review about several typical experiments and their results. Then based on the empirical study, especially the achievement of Güth et al. (1982) and Fischbacher et al. (2009), we have a full discussion on how competition affects social preferences in the context of a bargaining game.

Introduction

Economists have long been interested in the bargaining games. There is a considerable amount of literature published in this field by now. Firstly Neumann and Morgenstern (1944) studied bargaining games in the book The Theory of Games and Economic Behavior. The bargaining game is a kind of typical dynamic game and plays an essential role in game theory. In 1982, Rubinstein suggested bargaining games of alternating offers model which was based on the work of Stalh in 1972 and Krelle in 1976. Generally, it is regarded as the most classic literature about non-cooperative games theory.

Additionally, John Forbes Nash published two essays in 1950 and 1951 respectively, which were the turning point of non-cooperative games. His contribution about Nash equilibrium applied to solve game theory problems became the foundation for he won the 1994 Nobel Prize in economics, and the research is quite practicable and is applied in various fields. Then in 1986, Rubinstein et al (1986) made further research on bargaining games by analyzing the relationship between the static axiomatic and the dynamic strategic, which made a contribution to modify Nash bargaining solution.

At the end of 20th century, many economists began to concentrate on the impact of competition to bargaining game, and among them, what Roth et al. (1991) have done maybe the most typical one by making a series of experiments among four countries to find the bargaining and market behavior. After Roth, Fischbacher et al. (2009) conducted several specified experiments on the power of competition to proposers and responders with fairness, and they found that the outcome of responder’s average share of the pie would have a significant change by merely increasing small in competition levels. In view of all that has been mentioned so far, one may suppose that we first have a look at a famous bargaining game experiment.

The typical ultimatum game

One of many typical bargaining games is the ultimatum game.  In the standard experiment without competition, there are 2 parties X and Y. X, the proposer can decide how to distribute a fixed amount of money between them. Y, the responder could only accept or reject the proposal. If Y accepts, the distribution conducted and they will exactly get the amount proposed by X. Or, if Y chooses to reject the proposal, both of them would get a payoff of zero. Clearly under the rational person and purely self-interest hypothesis we can predict that the responder Y should accept any positive offer proposed by X. However, this prediction was rejected by the first experimental study of the ultimatum game (Güth, Schmittberger, and Schwarze, 1982) and numerous subsequent studies in the following years. One robust observation result we can summarize through these studies is that responders frequently reject low offers and most proposers offer between 30% and 50% of the surplus to their responders.

Why could this happen? There are two possible reasons for this behavior. One is that the proposer cares about fairness, which is to say that he prefers a fair allocation with a lower payoff to himself to an unfair allocation where he can get more. The other explanation is that he may choose to offer a fair allocation because he is afraid that an unfair proposal will be rejected by the responder. Which one is right or both of them matter? This question was answered by Forsythe, Horowitz, Savin and Selfton (1994) using a comparison of different behaviors in the Ultimatum game and the Dictator game.

Like in the ultimatum game, there are 2 parties X and Y. Player X can make a proposal on how to divide some money between himself and player Y. What is different to the ultimatum game is that in the dictator game the responder Y does not have the power to reject. The proposal is dictated by the proposer. If the proposer prefer a fairness allocation, the result in the dictator game should be similar to that in ultimatum game. However, they find that proposers are considerably more parsimonious in the dictator game. A significant fraction of dictators give nothing. This shows that many proposers are generous and fair only for strategic reasons in the ultimatum game. The fear of being rejected by the responders is the right explanation.

Introduction of Competition

How will competition influence the results in the above experiments? Since there are two different roles in the typical ultimatum game, we should consider two kinds of situation when we add the competition factor into bargaining game: proposer competition and responder competition.

1. Games with proposer competition

Roth et al. (1991) conducted an experiment about the ultimatum game with proposer competition in four countries (Israel, Japan, the United States and Yugoslavia). There are n-1 proposers who simultaneously propose a share 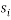to the only responder who can decide whether to accept the highest price 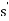or not. If the responder accepts it, his monetary payoff is 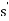and the successful proposer earns 1- 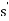. If the responder rejects 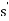, all players receive a payoff of zero. The results they get from the experiment are displayed in the Figure1 and Figure2. Though there are some little differences between the data in different countries, the price proposals, or say, the amounts of money accepted by the responders are much nearer the middle of the range.

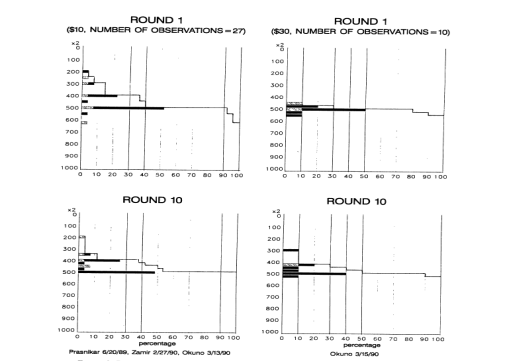
Figure 1 Distribution of bargaining offers in the US

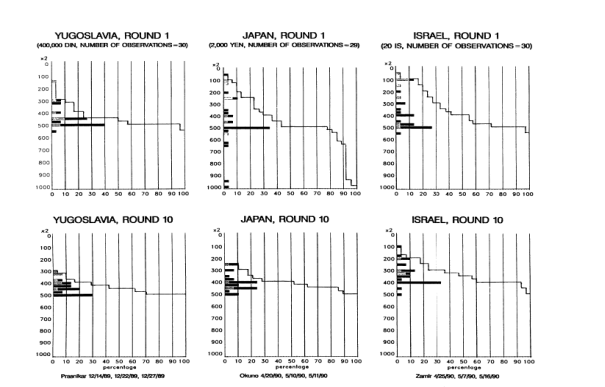
Figure 2 Distribution of bargaining offers in Yugoslavia, Japan and Isreal

2. Games with responder competition

Fischbacher et al., 2009 investigated the effects of competition on the outcomes of a bargaining game. They examined both the cases of proposer competition and responder competition.

Firstly they introduce proposer competition to the ultimatum game (UG) by adding one extra proposer (PC2), which causes a large increase in mean accepted offers. At the same time they find even under competition proposers still reap substantial share of the surplus. Obviously this result is approximately consistent with Roth’s.

Similarly they introduce responder competition to the ultimatum game (UG) by adding one extra responder (RC2), which causes a large reduction in mean accepted offers. Then adding three additional responders (by moving from RC2 to RC5) causes a further reduction in the mean accepted offer.

Figure 3 Average accepted offer in bargaining and market experiments

Showing clearly by the Figure, introducing competition to the UG has significantly large effects on the amount of accepted offer and the behavior of players in the experiments. The responder’s earnings in PC2 are almost twice as large as in the UG, while the trading responder in RC2 receives only 50% of the responder’s payoff in the UG. Why does the maximum offer size change a lot when the competition levels change? We can take the social preferences into consideration.

Preferences are choices people make under different situations. Social preferences are how people rank different allocations to themselves and others. There are many behaviors which we can use social preferences to explain, such as reciprocity, fairness, altruism, inequity aversion, etc.

References

Roth, A. E., Prasnikar, V., Okuno-Fujiwara, M., and Zamir, S., 1991, “Bargaining and Market Behavior in Jerusalem, Ljubljana, Pittsburgh, and Tokyo: An Experimental Study”, American Economic Review, vol. 81, no. 5, pp. 1068-1095

Güth, W. (1995). “On ultimatum bargaining experiments – A personal review. Journal of Economic Behavior & Organization”, vol. 27(3), pp.329-344.

Fischbacher, U., Fong, C. and Fehr, E. (2009). “Fairness, errors and the power of competition. Journal of Economic Behavior & Organization”, vol. 72(1), pp.527-545.

SCHMIDT, K. (2011). “Social Preferences and Competition. Journal of Money, Credit and Banking”, vol.43, pp.207-231.