Impact of Seismicity on Performance of RC Shear Wall
Impact of Seismicity on Performance and Cost of RC Shear Wall Buildings in Dubai, UAE
Mohammad AlHamaydeh, P.E., M.ASCE [1]; Nader Aly, S.M.ASCE [2]; and Khaled Galal, P.Eng., M.ASCE [3]
ABSTRACT
Unfortunately, available probabilistic seismic hazard studies are reporting significantly varying estimates for Dubai seismicity. Given Dubai’s rapid economic growth, it is crucial to assess the impact of the diverse estimates on performance and cost of buildings. This research investigates and quantifies the impact of the high and moderate seismicity estimates of Dubai on the seismic performance, construction and repair costs of buildings with 6, 9 and 12 stories. The reference buildings are made up of reinforced concrete with special shear walls as their seismic force resisting system. The seismic performance is investigated using nonlinear static and incremental dynamic analyses. Construction and repair costs associated with earthquake damages are evaluated to quantify the impacts. Results showed that designing for higher seismicity yields significant enhancement in overall structural performance. In addition, the higher seismicity estimate resulted in slight increase in initial construction cost. However, the increase in initial investment is outweighed by significant enhancements in seismic performance and reduction in earthquake damages. This resulted in overall cost savings when reduction in repair and downtime costs are considered.
Keywords: Seismic Hazard, RC Shear Walls, Seismic Vulnerability, Seismic Performance, Earthquake Losses.
Introduction and Background
The economy of UAE and specifically Dubai has been rapidly growing over the past few decades. Significant investments are taking place in the various sectors, especially in the real estate sector. In addition, in November 2014, Dubai was announced to be the hosting city of the coming EXPO 2020. As a result, substantial growth is taking place in the real estate sector. Several residential, commercial and hotel buildings are going to be designed and constructed to accommodate the increase in population size. This region suffers from considerable uncertainty in its seismicity level and the design guidelines that should be followed (AlHamaydeh et al., 2012). The seismicity level of UAE and Dubai has been the matter of several research studies, such as Abdalla and Al-homoud (2004), Aldama-Bustos et al. (2009) and Khan et al. (2013). Nevertheless, unfortunately there is not much consensus in these research studies about the seismicity levels that should be designed for in UAE. This could be attributed to the lack of in-depth seismological data and historical recordings of ground motions in this region. Such data would have been useful in providing comprehensive and sound seismic design guidelines (AlHamaydeh et al., 2013). The minimum seismic design requirements set by the local authorities in Dubai are based on the 1997 Uniform Building Code (UBC’97). However, the municipality has been proactive in adapting to tremors that were felt and measured in UAE in April, 2013. They sent a circular to consulting offices in May, 2013 raising the minimum requirement to zone 2B for buildings higher than nine stories and zone 2A for buildings between four to nine stories. Therefore, the unprecedented growth in the number of buildings in Dubai combined with the lack of consensus on seismic design criteria complicate the vulnerability to earthquakes. It is generally believed that the UAE has low seismicity. Nevertheless, over the past few years, a significant number of regional seismic activities, originating from faults surrounding the UAE, has been recorded by Dubai Seismic Network (DSN). Additionally, DSN has recorded some local seismic activities over the period from 2006 to 2014.
UAE seismicity is affected by earthquakes originating from near-fault and far-field seismic sources (Mwafy, 2011). The most recent seismic hazard study for UAE, available to the authors, was published in 2013 by Khan et al. (2013). The study provided a comprehensive probabilistic seismic hazard assessment and spectral accelerations for the entire UAE. Furthermore, it implemented a standardized earthquakes catalogue for UAE compiled from United States Geological Survey (USGS), National Geosciences of Iran (2015) and the National Center of Meteorology and Seismology of UAE (NCMS) (2015) that dates back to 110 years. Furthermore, Khan et al. (2013) have used seven different ground motion prediction equations incorporating three next generation attenuation equations due to the lack of specific equations for UAE. They attributed UAE seismicity to the seismic source zones shown in Figure 1. In addition, the seismic hazard study by Shama in 2011 highlighted several local crustal faults in UAE that might affect its seismicity level. These faults are Dibba, Wadi El Fay, Wadi Ham, Wadi-Shimal, Oman and West Coast fault (Shama, 2011). Unfortunately, the level of seismicity is not clearly set since there is no strong consensus among researchers about the exact seismic level of UAE or Dubai. On the other hand, reviewing the available probabilistic seismic hazard studies conducted for UAE and Dubai clearly shows that there are significant variations in the estimated seismicity levels. In fact, results vary from no seismic hazard to very high seismicity. Table 1 shows a summary of Peak Ground Accelerations (PGA) from several probabilistic seismic hazard studies. The reported PGAs vary from less than 0.05g to 0.32g. This is attributed to the differences in the used source zonation, recurrence parameters, earthquake catalogues and ground motion prediction equations. The differences are mainly due to the lack of detailed seismological measurement and data in this region and such data is required to provide a comprehensive and sound seismic hazard study (AlHamaydeh et al., 2013). The variation in seismicity was a driving factor for many research studies related to the impact on design of buildings in Dubai, such as (AlHamaydeh et al., 2010; AlHamaydeh et al., 2011; and AlHamaydeh and Al-Shamsi, 2013).
The objective of this paper is to investigate the impact of the seismicity hazard level on the performance, construction, repair and downtime costs of reinforced concrete (RC) shear wall buildings in Dubai. In this regard, six RC shear wall buildings are designed and detailed following the 2012 International Building Code (IBC’12) standards. The reference buildings are 6-story, 9-story and 12-story. They are chosen to target the main sectors of buildings inventory in Dubai, UAE. These buildings are designed for two different seismic hazard levels that represent high and moderate seismicity estimates of Dubai. The different designs are compared based on their seismic performance, construction and repair costs in order to investigate and quantify the impact of the seismic design level. The seismic performance is evaluated following the methodology outlined in FEMA P695, which is a technical publication aiming to establish standard procedures for quantifying the seismic performance factors of buildings (Federal Emergency Management Agency (FEMA), 2009). The assessment methodology is based on nonlinear pseudo-static and dynamic analyses. The nonlinear response history analyses are performed using a set of ground motion records selected and scaled to represent the highest possible seismic activity in Dubai. As such, this would highlight the implications on design, seismic performance, construction and repair costs of RC shear wall buildings designed for different seismic hazard levels in Dubai, if the high seismicity estimate turns to be the most realistic. In addition, total construction cost is estimated considering structural and non-structural components. Finally, the repair cost is evaluated based on the structural and non-structural damage percentages adapted from SEAOC blue book (Structural Engineers Association of California, 1999).
Details of the Reference Buildings
The six reference buildings considered in this paper are intended to represent typical office buildings located in Dubai, UAE. The buildings have number of floors ranging from 6 to 12 stories to represent the majority of common buildings in Dubai. They are made up of RC and have a typical floor plan as shown in Figure 2. The plan consists of five 6m (20ft) bays and total dimensions of 30mx30m (100ftx100ft). Furthermore, the overall structural height varies between 24m to 48m (78ft to 156ft); with a typical floor height of 4m (13ft). The lateral force resisting system consists of special RC shear wall placed along the perimeter of the building. This arrangement ensures that center of mass is close to center of rigidity, hence it avoids inherent torsional effects. In addition, placing the walls along the perimeter boosts the building torsional resistance and reduces the shear demands on walls due to accidental torsion effects.
The gravity system consists of RC square columns, while the floor system comprises of cast-in-situ flat plate. However, the gravity system is not designed to be part of the lateral force resisting system. It is only designed to support vertical loads and to satisfy the deformation compatibility requirement. For design purposes, concrete compressive strength (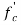 ) is assumed to be 28MPa (4.0ksi) for columns and slabs, and 38MPa (5.0ksi) for shear walls. Additionally, the yield strength (fy) of reinforcement is assumed to be 420MPa (60ksi). Super Imposed Dead Load (SDL) is 3.6kPa (75psf), excluding the self-weight of the concrete slabs. This SDL value is a conservative estimate commonly used for office buildings in Dubai. The breakdown of this estimate is as follows: 2 kPa (for 100mm of leveling screed and flooring tiles), 1 kPa for partitions (usually movable partitions) and 0.6 kPa allowance for mechanical, electrical and plumping overhanging services. Curtain wall (cladding) load on the perimeter of each floor is 0.72kPa (15psf). Moreover, for office buildings the typical floors live load is 2.4kPa (50psf) and the roof live load is 1kPa (20psf) as per ASCE7-10.
) is assumed to be 28MPa (4.0ksi) for columns and slabs, and 38MPa (5.0ksi) for shear walls. Additionally, the yield strength (fy) of reinforcement is assumed to be 420MPa (60ksi). Super Imposed Dead Load (SDL) is 3.6kPa (75psf), excluding the self-weight of the concrete slabs. This SDL value is a conservative estimate commonly used for office buildings in Dubai. The breakdown of this estimate is as follows: 2 kPa (for 100mm of leveling screed and flooring tiles), 1 kPa for partitions (usually movable partitions) and 0.6 kPa allowance for mechanical, electrical and plumping overhanging services. Curtain wall (cladding) load on the perimeter of each floor is 0.72kPa (15psf). Moreover, for office buildings the typical floors live load is 2.4kPa (50psf) and the roof live load is 1kPa (20psf) as per ASCE7-10.
The six reference buildings are designed and detailed according to IBC’12 requirements for two different seismic hazard levels representing high and moderate seismicity estimates in Dubai. The selection of the two seismic design levels is driven by the existing uncertainty in seismic loading and the substantial variability in reported seismic hazard levels for UAE and Dubai. Therefore, it is deemed a reasonable choice for the objective of this paper to consider the highest and moderate seismicity levels. This would allow investigating the consequences of the possible alternative seismic loading levels available to designers. The highest seismicity level represents the upper bound, and it is obtained from USGS (2015). The USGS seismic hazard level for Dubai estimate is selected in this study (i.e. Ss = 1.65g and S1 = 0.65g). Moreover, the moderate seismic design level represents Abu Dhabi International Building Code 2011 (ADIBC’11) estimate for Dubai. The elastic design response spectra for the two considered seismicity levels along with the ASCE7-10 estimated fundamental periods of the studied six buildings are presented in Figure 3. As shown, at each seismic design level, three buildings with 6-stories, 9-stories and 12-stories are designed with special RC shear walls. Summary of all buildings’ details including response modification factors (R and Cd), design spectral accelerations and elastic fundamental time periods, and approximate periods’ upper limit are given in Table 2. It is worth mentioning that the ground motion input parameters (Ss and S1) of the two seismicity levels (high and moderate) result in Seismic Design Category (SDC) D for the six considered buildings. Consequently, ordinary RC shear walls are not permitted by the design code (i.e. ASCE7-10). Thus, all buildings are required to have special RC walls. Furthermore, choosing special detailing for both seismicity levels would allow investigating the direct impact of the seismic design level on the cost and performance of walls with same level of detailing requirements. The buildings are given a legend showing its ID (i.e. Building1 to Building6), number of stories (i.e. 6Story, 9Story or 12Story), seismic design level (i.e. High or Moderate) and shear wall type (i.e. Special or Ordinary). A site class D is assumed for the six reference buildings. This assumption complies with IBC’12 recommendations.
Design Summary
The buildings are designed and detailed in accordance to IBC’12 standards which refers to ASCE7-10 for minimum design loads and ACI318-11for structural concrete requirements. The designs implement the state of the art practices in design and construction followed in Dubai, UAE. For the design purposes, elastic analysis is done using 3D models on CSI ETABS commercial package (“ETABS,” 2015). To determine the majority of the seismic mass, the gravity system is designed first and fixed for the three buildings.
The gravity system is designed to resist axial forces from all vertical loads in addition to the moments and shears induced from deformation compatibility requirements. In order to ensure the structural stability of gravity columns, they are designed to resist the induced actions (bending moments and shear forces) from the deformations that will be imposed by earthquake excitations on the building. The bending moments and shear forces are estimated based on the maximum allowable inter-story drift by IBC’12 which is 2%. The stiffness of the columns is estimated using ETABS by applying a force at the top and bottom of the considered story and by getting the corresponding displacement. The shear forces are then calculated by multiplying the maximum allowable displacement by the stiffness of each column. Then from the shear force, the moment is calculated as shown in Equations (1) and (2).
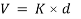 Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â (1)
                                                                                      (1)
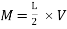 Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â (2)
                                                                                          (2)
Where V is shear force, d is displacement (calculated using ETABS), M is bending moment and L is column height. It should be noted that concrete shear capacity is found sufficient to resist the shear forces due to imposed deformations by applied seismic forces. Therefore, minimum lateral reinforcement (i.e. column ties) is provided in columns with reference to clause 7.10 in ACI318-11. The gravity system components (i.e. flat plates and columns) are designed in accordance to ACI318-11 provisions using in-house design spreadsheets. For an optimized design, following common design trends in UAE, columns cross sections and reinforcement are grouped and changed every three floors. The gravity system is common between buildings with the same number of floors. The gravity columns design details for the six reference buildings are summarized in Figure 4. Figure 4 (a), (b) and (c) show the dimensions and reinforcement details of the 6- , 9- and 12-story buildings, respectively. On the left side of each Figure, the columns’ cross section dimensions are provided over each group of floors. The right side shows the vertical and horizontal reinforcement of the different columns (i.e. columns around the opening and remaining columns) in each group of floors. The minimum required slab thickness is calculated such that it satisfies ACI318-11 Table 9.5(c) minimum requirements. For the longest clear span of 5.3m, the minimum required thickness is 177mm. This figure is rounded up and 200mm thick flat plates are used. The flat plates are reinforced with T16 reinforcement bars spaced at 125mm, top and bottom in both directions. Additional T20 reinforcement spaced at 125mm (2m long) are added on top of columns in both directions.
The lateral system is designed to resist the seismic lateral loads determined according to IBC’12 Static Equivalent Lateral Force (SELF) method. The SELF method is permitted for all the six reference buildings. This is because the total height for all buildings does not exceed 48m (160ft), the SDC is D and no structural irregularities exist according to ASCE7-10, Table 12.6-1. Linear static analysis is performed using ETABS to evaluate the induced forces and displacements from seismic forces. Then, shear walls are designed to satisfy strength and drift requirements. Inter-story drift ratios are controlled within code, IBC’12, limits (2%) by varying the shear wall stiffness through changing its in-plan length. Strength requirements are satisfied by designing the shear walls for the induced bending moments and shear forces by the seismic actions using Quickwall software (“Quick Concrete Wall,” 2015). Shear walls’ thickness and reinforcement are changed every three floors to optimize the design and to match common design practices in Dubai. However, walls’ in-plane length is kept constant throughout the buildings height to avoid any vertical structural irregularities. The need for specially detailed boundary elements is checked every three floors using the displacement-based approach. The use of displacement based approach for checking the boundary elements vertical extent is preferred over the use of stress-based approach. This is because the latter approach was proven to provide highly conservative requirements for the special detailing (Wallace and Moehle, 1992) and (Thomsen IV and Wallace, 2004). For practical constructability, boundary elements are designed to have the same wall thickness. Additionally, to comply with ACI318-11 minimum thickness requirements and conform to typical design practices in the UAE, an aspect ratio of at least 25.4mm: 304.8mm (1in: 12in) is maintained between wall thickness and length. The walls’ minimum thickness depends on the unsupported height and length. Therefore, as the walls’ unsupported heights across the different buildings are constant (i.e. limited by the typical story height), it is necessary to impose a practical criterion on the walls’ thickness as we change the length from building to building. This approach guarantees that the different designs are subjected to the same guidelines, especially for sizing the walls’ cross sections. This would result in a fair response comparison among all designs as they follow similar basis that imitates typical design practices in the UAE. During initial dynamic analyses of the 12-story buildings, B5-12S-H-S and B6-12S-M-S, it was observed that the critical section was not at the walls’ base. This is contradicting the code assumption of having a single critical section at the base of cantilevered shear walls. The critical section resulting in the dynamic analysis was actually shifted from the wall base to the bottom of the lowest floor in upper quarter of the building (10th floor). The initiated failure mechanism was governed by higher modes effects and the formation of plastic hinges at upper floors. The optimization done initially to the design by reducing dimensions and reinforcement for upper floors magnified the impact of higher modes effects. As a result, it triggered the failure and plastic hinge formation to be initiated at the reduced cross section. Therefore, the critical section became located at the weak spot at higher levels, which resulted in an unfavorable premature collapse mechanism. This observation has been highlighted by previous researchers, such as Tremblay et al. (2001), Bachmann and Linde (1995), and Panneton et al. (2006). It was also experimentally proven by shake table and cyclic loading tests (El-Sokkary et al., 2013). As an example, the modal analysis of the 12-story building, B5-12S-H-S, is shown in Table 3. It can be seen that there are clear separations between the individual modes’ characteristics (periods and modal masses). This is generally expected in a flexural cantilever structural type (i.e. shear walls). The first mode effective mass is usually ranging from 50% to 70% and the second mode period is approximately one sixth of the first mode. This is consistent with many research studies which investigated the effects of higher modes on response of cantilever shear walls (e.g. Humar and Mahgoub, 2003 and Tremblay et al., 2001). Furthermore, it is clear that relative modal weights (%) and modal participation factors are relatively high at 7th, 8th and 12th vibration modes which highlights the impact of higher modes. As a result, the design was revised by keeping the cross section and reinforcement constant for the upper half of the 12-story (B5-12S-H-S and B6-12S-M-S) and 9-story buildings (B3-9S-H-S and B4-9S-M-S). For 6-story buildings (B1-6S-H-S and B2-6S-M-S), a single cross-section was used for all floors with terminating boundary element at third floor. This conforms to the state-of-art design and construction practices in Dubai, UAE. It also matches the design philosophy adopted in other 12-story and 9-story buildings by keeping the same cross section and reinforcement for upper six floors. Summary of the shear walls design details is shown in Figure 5.
Nonlinear Modeling
The six reference buildings are modeled using lumped plasticity formulations on IDARC-2D (Reinhorn et al., 2009). Since the buildings are symmetric, mass participation of torsional modes of vibration are low. Therefore, torsional effects are negligible and a two-dimensional model is sufficient to simulate the buildings’ response. The shear walls are idealized using macro-models by representing the structural members with equivalent elements possessing all nonlinear characteristics. The members’ nonlinear characteristics depend on distribution of plasticity and yield penetration. A lumped plasticity model consisting of two nonlinear rotational springs located at the ends and an elastic member is used for the shear walls. The nonlinearity is concentrated at the locations of the nonlinear rotational springs. The flexural and shear deformations of the shear walls are modelled using the tri-linear (three parameter) hysteretic model developed by Park et al. (1987). The tri-linear hysteretic models allow controlling the stiffness degradation and strength deterioration due to ductility and energy. In addition, the axial deformations of the shear walls are considered by a linear-elastic spring. For the shear walls, the moment-curvature and shear-distortion are calculated using the fiber elements procedure of IDARC2D. The wall cross section is divided into number of fibers and then subjected to increments of curvatures. From strain compatibility and equilibrium, the strains are calculated and used to compute the resulting axial forces and bending moments in the section (Reinhorn et al., 2009).
Results and Discussion
The buildings’ seismic performance is evaluated following FEMA P695 methodology (2009). FEMA P695 approach is based on nonlinear pseudo static (pushover) analysis, Incremental Dynamic Analysis (IDA) and fragility analysis. Pushover analysis is used to validate the nonlinear model and estimate the period based ductility of the buildings. Then, IDA analysis is performed using a suite of far-field ground motion records to estimate the median collapse intensity and collapse margin ratio. The far-field ground motion records are scaled to match the MCE response spectrum of the highest seismicity estimate in UAE. This seismicity hazard level is as estimated by USGS (2015) for Dubai (Ss = 1.65 g and S1 = 0.65 g). The selected scaling level simulates the worst, yet possible seismic hazard scenario from distant sources (e.g. Zagros thrust or Makran subduction zone) as highlighted by Sigbjornsson and Elnashai (2006). Thus, it allows assessing the consequences of the selected seismic design level (i.e. high or moderate) on the seismic performance, construction and repair costs of RC shear wall buildings in Dubai. The calculated collapse margin ratios from the IDA are adjusted to account for uncertainties in design basis, test data, nonlinear modeling and to consider the spectral shape of the ground motion records. The spectral content is accounted for based on the calculated period based ductility. Adjusted IDA results are finally used to calculate exceedance probabilities for ASCE-41 (2013) performance levels, Collapse Prevention (CP), Life Safety (LS) and Immediate Occupancy (IO).
Nonlinear Pseudo-Static (Pushover) Analysis
Pushover analysis is performed using an inverted triangle displacement profile as a pushing function for all buildings. The intensity is increased monotonically until the ultimate base shear degrades by 20%. The results are used to construct capacity curves (back-bone) for the reference buildings in the form of roof drift ratio versus base shear coefficient (i.e. base shear normalized by seismic weight). Pushover capacity curves are used to assess the buildings deformation and strength capacities.
The capacity curves of the three buildings designed for the high seismicity estimate (i.e. B1-6S-H-S, B3-9S-H-S and B5-12S-H-S) are shown in Figure 6. Normalized base shear capacities are 0.57, 0.5 and 0.46 for B1-6S-H-S, B3-9S-H-S and B5-12S-H-S, respectively. As expected, base shear capacity is higher for the shorter building (6-story). This is attributed to the higher design forces which resulted from the relatively higher initial stiffness of squat shear walls compared to their slender counterpart. B1-6S-H-S reached a maximum roof drift ratio, prior collapse, of 6.5%, while B3-9S-H-S reached 6% and B5-12S-H-S reached 7.25%. The three buildings have period-based ductility calculated as recommended by FEMA P695 greater than 8. It can also be observed that in the three high seismicity designs, the capacity curves do not experience severe degradation in strength or deterioration in stiffness. This matches the expected behavior of well detailed special RC shear walls with confined boundary elements. It is noticed from the final damage states of the buildings, at 20% strength degradation, that static pushover analysis resulted in a failure mode at the base of the shear walls conforming to the design code assumed critical section. The overall structural damage index reported by IDARC-2D is 0.359, 0.426 and 0.618 for B1-6S-H-S, B3-9S-H-S and B5-12S-H-S. It is worth mentioning that these damages are concentrated at first floor shear walls.
Established capacity curves for buildings designed for moderate seismicity (B2-6S-M-S, B4-9S-M-S and B6-12S-M-S) are presented in Figure 6. From shown capacity curves, normalized base shear capacities are 0.31, 0.26 and 0.24 for buildings B2-6S-M-S, B4-9S-M-S and B6-12S-M-S, respectively. Similar to the high seismicity design, the 6-story building has the highest normalized base shear capacity. This is due to its lateral system (shear walls) relatively higher stiffness which resulted in higher demands. Maximum drift ratios, prior collapse achieved by B2-6S-M-S, B4-9S-M-S and B6-12S-M-S are 9.25%, 8% and 3.5%, respectively. The three designs have period-based ductility greater than 8 calculated as recommended by FEMA P695. The overall structural damage index reported by IDARC-2D is 0.371 for B2-6S-M-S, 0.455 for B4-9S-M-S and 0.359 for B6-12S-M-S. These damages are triggered at the first floor shear walls only. Therefore, similar to high seismicity designs, the pseudo static pushover analysis results of moderate seismicity designs suggests a single critical section at the wall base. This conclusion matches with design code recommendation for regular buildings permitted to be designed following the static method (SELF) by ASCE7-10.
Nonlinear Incremental Dynamic Analysis (IDA)
The seismic performance of the reference buildings is investigated under the random nature of earthquakes. Standard nonlinear pseudo-static analysis does not inherently fully capture the higher modes effects which usually govern the response of tall and irregular buildings. Consequently, the use of nonlinear dynamic analysis is more appropriate in such cases. IDA provides better insight of the expected structural response from the linear range through the nonlinear response and until it losses stability and collapse (Vamvatsikos and Cornell, 2004). The IDA in this case is performed using a very fine increment of 0.1g for the spectral accelerations. The increments are increased until all ground motion records caused the buildings to collapse or exceed the CP maximum drift ratio limit of 2% as specified by ASCE-41. However, the maximum spectral acceleration for all the records is not increased more than 2.5g. The total number of dynamic analysis runs performed for each reference building is around 1100 (22 records x 2 components x 25 scale factors).
Figure 7 presents the resulting IDA curves for high seismicity designs, B1-6S-H-S, B3-9S-H-S and B5-12S-H-S. The structural response derived from IDA curves can depend to some extent on the characteristics of the particular accelerograms used. Thus, the performance is judged based on a suit of ground motion records to segregate this effect. On average, at low drift ratios (approximately up to 1%), the three designs (B1-6S-H-S, B3-9S-H-S and B5-12S-H-S) exhibit a linear behavior. The same linear behavior is resulting from some of the ground motion records up to the MCE spectral acceleration. At higher spectral accelerations, the structural response starts to vary showing several patterns of nonlinearities, such as softening, hardening and weaving. For only few records, the structure seems to soften and move to large drifts rapidly until it reaches collapse. Collapse in these curves, whether resulting from convergence issues, numerical instabilities, or very large drift ratio, is represented using a drift ratio of 10% and a flat line in IDA curves. Majority of the earthquake records caused severe hardening and weaving around the elastic response. The weaving observation conforms to the common equal displacement rule stating that inelastic and elastic displacements are equal for structures with relatively moderate time periods (Vamvatsikos and Cornell, 2002). In addition, for some records, the hardening phenomenon in which the structure seems to perform better at higher intensities is somewhat against the common expectation (Vamvatsikos and Cornell, 2002). This is because generally the time and pattern of the time-history governs the response more than just the intensity. Moreover, the upward scaling done to the records makes the less responsive cycles at the beginning of the time-history strong enough to cause damage and yielding of the structural elements. Therefore, some strong ground motion records at some intensity might cause early yielding of a specific floor, usually a low floor. This floor acts as a sacrificial fuse which reduces the response of higher floors (Vamvatsikos and Cornell, 2002). Another very interesting observation that is clearly seen in IDA curves shown in Figure 7 is what is called “Structural Resurrection.” This phenomenon has been observed by Vamvatsikos and Cornell (2002) and is defined as a severe hardening behavior. In structural resurrection, the building moves all the way to complete collapse (numerical instability or convergence issues) at some intensity. Then at higher intensities it shows a lower or higher response, but without collapsing. This happens because the time and pattern of the ground motion record at a particular intensity might be more damaging than at higher intensities. In other words, this particular intensity causes the structure to resonate. This is observed in the three designs, but more often in shorter buildings; B1-6S-H-S (6-story) and B3-9S-H-S (9-story) compared to the 12-story building (B5-12S-H-S). The median collapse intensity (ÅœCT); the spectral acceleration at which 50% (22) of the records caused the structure to collapse, is 1.38g, 0.76g and 0.70g for B1-6S-H-S, B3-9S-H-S and B5-12S-H-S, respectively. Moreover, it can be observed from Figure 7 that for building B1-6S-H-S there is a number of flat lines representing collapse from individual ground motion records above the MCE level (SMT). This indicates that the 6-story building designed for high seismicity shows collapse due to several ground motion records, excessively large drift ratios and global instabilities, at spectral accelerations much higher than MCE level. For buildings B3-9S-H-S and B5-12S-H-S the number of flat lines above MCE is relatively lower compared to B1-6S-H-S. Comparing the median collapse intensity (ÅœCT) to MCE level (SMT), the Collapse Margin Ratio (CMR) is 1.13, 0.84 and 0.96 for B1-6S-H-S, B3-9S-H-S and B5-12S-H-S, respectively. Based on CMR, only the 6-story building design (B1-6S-H-S) has an acceptable collapse margin more than 1. However, the CMR has to be adjusted to account for sources of uncertainties and spectral shape of ground motion records before being used to judge the structural performance. The adjusted values for CMRs are shown in the next subsection. It should be noted that the MCE level (SMT) refers to the highest seismicity estimate level. This is particularly chosen to achieve the objectives of this research of investigating the performance, construction and life cycle cost of the different designs under the high seismic hazard that might be present in Dubai, UAE. This scenario will simulate a conservative possible seismic hazard in Dubai and its consequences on performance of buildings designed for two different seismic hazard levels.
Figure 8 depicts IDA curves for moderate seismicity designs (B2-6S-M-S, B4-9S-M-S and B6-12S-M-S). IDA curves show that, on average, the three designs exhibit a linear behavior at low drift ratios except for some ground motion records in which the structure remains linear up to significantly high spectral accelerations. At higher spectral accelerations, most records show nonlinear structural response, such as softening, hardening and weaving. Mainly significant weaving is observed in the three designs and in some cases structural resurrection is noticed. It is interesting to highlight that structural resurrection is most observed in the 6-story building (B2-6S-M-S) and least observed in the 12-story building (B6-12S-M-S). Median collapse intensity (ÅœCT) is 0.78g for B2-6S-M-S, 0.51g for B4-9S-M-S and 0.48g for B6-12S-M-S. Furthermore, calculated CMRs are 0.64, 0.56 and 0.66 for B2-6S-M-S, B4-9S-M-S and B6-12S-M-S, respectively. None of the three designs have any margin of safety against structural collapse based on CMRs. However, decision about performance cannot be made completely based on CMRs without doing the proper adjustments. The adjusted CMRs are presented in following subsection.
Fragility Analysis
The seismic vulnerability of the different designs is assessed using fragility curves relating the probabilities of exceeding a performance level to the spectral acceleration demand. IDA results are first used to calculate the probabilities of exceeding the three performance levels (i.e. IO, LS and CP) at every spectral acceleration. Based on the analytically calculated probabilities a fragility function is derived. The derived fitting fragility curve is based on a cumulative distribution function following the maximum likelihood method by Baker (2015). This method estimates fragility parameters (i.e. mean and standard deviation/dispersion) to produce a fragility distribution that would most likely re-produce observed data. The fitted fragility functions are then adjusted according to FEMA P695 to account for record-to-record (βRTR), design basis (βDR), test data (βTD) and modeling uncertainties (βMDL). In this case, record to record uncertainty (βRTR) is given a fixed value of 0.4 for the chosen far-field records set. Moreover, there is high confidence in the basis of design requirements since the buildings are designed according to IBC’12 relevant standards. Hence, From Table 3-1 in FEMA P695, a value of 0.2 is selected for the design basis uncertainty (βDR), this corresponds to a medium completeness and robustness. For the lateral system used (i.e. special RC shear walls), the materials, components, assembly and system behaviour are well understood and documented. Thus, from Table 3-2 in FEMA P695 (2009), the test data uncertainty (βTD) is given a value of 0.2 corresponding to a medium completeness and robustness and high confidence in test results. Finally, corresponding to medium representation of collapse characteristics, high accuracy and robustness of nonlinear analysis models, the nonlinear modeling uncertainty (βMDL) is given a value 0.2. This is obtained from Table 5-3 in FEMA P695 (2009). The nonlinear modeling is performed using IDARC-2D which accounts for plastic hinge and crack formation in all structural elements. It also accounts for shear, axial and flexural deformation in structural members. However, the nonlinear analysis using IDARC-2D is limited to 2-Dimensions. Combining the different uncertainty parameters, using Equation (3), gives a total system collapse uncertainty (βTOT) of 0.525.
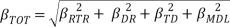 Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â (3)
                                                         (3)
The total system collapse uncertainty is used to adjust the fragility curves for the three performance levels. However, for the collapse fragilities, the adjusted probabilities are also multiplied by the Spectral Shape Factor (SSF) to account for the natural period elongation prior collapse. SSF is given in Tables 7-1a and 7-1b in FEMA P695 based on seismic design level, fundamental period of the structure and period-based ductility.
Analytical, log-normal fitted and adjusted collapse fragility curves for buildings B1-6S-H-S, B3-9S-H-S and B5-12S-H-S (high seismicity designs) are shown in Figure 9. Collapse is defined in FEMA P695 as either when the structure reaches excessive lateral drift (global dynamic instability) or through limit state criteria. In this study, the latter option is adopted in creating collapse fragility curves. Therefore, collapse in this case is defined as exceeding the drift ratio limit of CP Limit state of ASCE41. The adjusted median collapse intensity (SCT) is 1.92g, 1.1g and 1.07g for buildings B1-6S-H-S, B3-9S-H-S and B5-12S-H-S, respectively. ACMRs are evaluated using the adjusted median collapse intensity (SCT) and SMT. The calculated ACMR is 1.57 for B1-6S-H-S, 1.23 for B3-9S-H-S and 1.47 for B5-12S-H-S. This indicates 57%, 23% and 47% margin of safety against collapse for buildings B1-6S-H-S, B3-9S-H-S and B5-12S-H-S, respectively. Similarly, collapse fragility curves for B2-6S-M-S, B4-9S-M-S and B6-12S-M-S (moderate seismicity designs) are given in Figure 10. Adjusted median collapse intensity (SCT) is 1.09g, 0.75g and 0.69g for buildings B2-6S-M-S, B4-9S-M-S and B6-12S-M-S, respectively. Moreover, ACMR, ratio between SCT and SMT, is 0.89 for B2-6S-M-S, 0.82 for B4-9S-M-S and 0.95 for B6-12S-M-S. This reflects that the three moderate seismicity designs have no margin of safety against collapse.
IO, LS and CP fragility curves are given in Figure 11 for the six reference buildings. In general, it is observed that at the three performance levels fragility curves are much steeper for the buildings designed for moderate seismicity. This reflects higher exceedance probabilities compared to the buildings designed for high seismicity which have much flatter fragility curves. Additionally, At MCE level (SMT), B1-6S-H-S has 20% probability of exceeding CP limits state, 66% of exceeding LS limit state and 95% it exceeds IO performance level. On the other hand, B2-6S-M-S has 58% probability of exceeding CP performance level, 96% probability of exceeding LS and 100% probability of exceeding IO. Similarly, for B3-9S-H-S at the MCE level (SMT), the probabilities are 34%, 71% and 97% of exceeding CP, LS and IO, respectively. While B4-9S-M-S has 64%, 97% and 100% probabilities of exceeding CP, LS and IO damage states, respectively at MCE level. Finally, B5-12S-H-S has a 23% probability of exceeding CP, 64% of exceeding LS and 94% of exceeding IO at the MCE level. Conversely, B6-12S-M-S has 54% probability of exceeding CP, 85% probability it exceeds LS and 99% probability of exceeding IO. It is interesting to note that the superior performance of high seismicity designs is more evident at LS and CP performance levels.
Construction and Maintenance Cost Comparison
The impact of the seismic design level on the construction and repair costs is quantified. This quantification provides more tangible measures for the engineers and decision makers. For the objective of this study, focus is given to the earthquakes direct economic losses in terms of repair costs associated with structural and non-structural damages. Therefore, indirect costs, content repair or replacement costs are excluded. The total construction cost is estimated based on the cost of structural materials (i.e. concrete and reinforcement steel) and nonstructural components cost. Structural materials cost is approximated using average market unit prices, while nonstructural cost is taken as 55% of the total construction cost. Table 4 presents a summary of reference buildings construction cost. It should be noted that this cost only represents the skeleton construction cost, considering the superstructure and non-structural elements. It does not account for substructure cost, other construction costs and the contractor’s profit, etc. This is done to isolate other factors and focus on the seismic design level impact on construction and repair costs. Non-structural components’ cost in most office buildings is a significant portion of total cost. Therefore, majority of potential damage and losses from earthquakes are expected to occur in non-structural components. This is consistent with the recommendation of Taghavi and Miranda (2003) for including the impact of non-structural components cost on total construction cost and response assessment.
As expected, there is an increase in the construction cost of the buildings designed for the high seismicity estimate. However, the increase is only 9% for 12-story buildings and 6% for 6 and 9-story buildings.
Repair cost is calculated based on structural and non-structural damage percentages adapted from SEAOC blue book. SEAOC blue book performance levels, its description and damage percentages are summarized in Table 5. It can be seen that SP2/NP2 corresponds to IO performance level, SP3/NP3 parallels LS performance level and SP4/NP4 is equivalent to CP performance level. From the range of non-structural damage ratios provided by SEAOC blue book, the lower bound is chosen. The selection is based on experience since the reference buildings’ lateral system consists of shear walls which are relatively more rigid compared to other structural systems. The structural and non-structural repair costs are calculated using HAZUS economic losses estimation methodology (Federal Emergency Management Agency, 2010) as follows:
Structural Repair Cost ($) = [Structural material cost x Probability of  exceeding a limit state at MCE level x Structural damage ratio at the limit state]
Non-Structural Repair Cost ($) = [Non-structural cost x Probability of exceeding a limit state at MCE level x Non-Structural damage ratio at the limit state]
The calculated repair costs at the three performance levels along with the total construction costs are shown in Table 6. It is observed that at IO performance level, repair and construction costs are higher for the buildings designed for high seismicity (i.e. B1-6S-H-S, B3-9S-H-S and B5-12S-H-S). This conclusion is valid for 6, 9 and 12-story buildings. Nevertheless, at LS and CP the moderate seismicity designs (i.e. B2-6S-M-S, B4-9S-M-S and B6-12S-M-S) have higher repair and construction costs. The increase in repair costs at IO performance level when the buildings are designed for the higher seismicity estimate is in the range of 5-10%. However, the reduction in repair cost is ranging between 14% to 25% at LS and 42% to 63% at CP performance level. This reflects net cost saving associated with designing for a conservative seismic hazard estimate at LS and CP performance levels. The higher repair also indirectly reflects an increase in downtime of the structure.
Summary and Conclusions
This paper investigates the seismic hazard level impact on the performance and overall cost of buildings in Dubai. The investigation targets 6-story, 9-story and 12-story buildings located in Dubai and representing the main inventory of buildings. The selected reference buildings are designed and detailed following the state of the art design and construction practices in Dubai based on IBC’12. The buildings’ lateral force resisting system consists of special RC shear walls. The seismic performance and collapse safety of the reference buildings are investigated using nonlinear pseudo-static and dynamic analyses, namely pushover analysis and IDA, based on FEMA P695 methodology. The nonlinear analyses are performed using a fully detailed fiber-based finite element model developed on IDARC-2D. Large number of nonlinear analyses is performed to capture the buildings’ response due to seismic loads. Performance quantification is based on pushover capacity curves, ACMRs, seismic vulnerability and probabilities of exceeding IO, LS and CP at MCE. Finally, the impact of the seismic performance enhancement, due to choice of seismic design level, on the total cost is evaluated. This considered the net effect of construction, repair and downtime costs to present more realistic and solid conclusions.
Nonlinear response history analysis of preliminary optimized designs revealed unfavorable response for all reference buildings. An undesirable collapse mechanism caused by higher modes effects is noticed. This resulted in imposing greater demands at upper floors with reduced cross sections. Therefore, designs were revised to consider both enhancing the expected seismic performance and optimizing the construction cost. It is noteworthy that initial designs strictly followed the code design approach. Based on the static method outlined in the design code (IBC’12), cantilevered shear walls are expected to have a single critical section at the base. Yet, the dynamic analysis results showed that the critical section causing the collapse was shifted to upper floors with reduced sections. This is particularly clear in 9-story and 12-story buildings, which are more flexible structures compared to 6-story buildings.
Based on pushover capacity curves, as expected, all reference buildings showed a ductile response. However, the buildings designed for the high seismicity estimate of Dubai exhibited enhancements in their strength and inelastic deformation capacities. The calculated ACMRs reflected sufficient margin of safety (i.e. more than 20%) against collapse at MCE for the buildings designed for higher seismicity. On the other hand, moderate seismicity designs showed no margin of safety against collapse at MCE level. Furthermore, when the buildings are designed adapting the conservative seismicity estimate, there is a clear enhancement in their seismic vulnerability. This is clear in the flatter fragility curves for high seismicity designs at IO, LS and CP performance levels. The probabilities of exceeding IO, LS and CP at MCE are significantly reduced when the high seismic design level is chosen compared to the moderate design level. These clear enhancements in seismic performance resulting from the higher seismic design level is associated with limited increase (i.e. 6-9%) in initial construction cost. However, the total cost, considering the net effect of construction and repair costs, is reduced for higher seismicity designs at LS and CP performance levels. Therefore, the increase in initial investment associated with designing for conservative seismicity level is outweighed by the enhancement in seismic performance, and the reduced repair and downtime costs. Under the idealized conditions and modeling assumptions, these conclusions are applicable for typical buildings ranging between 6 and 12 stories. The main focus of this study was given to the impact of seismic design level on overall cost considering cost of superstructure and non-structural components. In fact, non-structural components cost contributes to the majority of total construction and potential repair costs. Hence, impact of seismic design level on other costs such as foundation cost is beyond the scope of this study.
References
Abdalla, J. A., and Al-homoud, A. (2004). Seismic Hazard Assessment of United Arab Emirates and its surroundings. Journal of Earthquake Engineering, 8(6), 817-837.
ADIBC’11 (Abu Dhabi International Building Code). (2011), Abu Dhabi Department of Municipal Affair, and International Code Council, Abu Dhabi, UAE.
Al Haddad, M., Siddiqi, G. H., Al Zaid, R., Arafah, A., Necioglu, A., & Turkelli, N. (1994). A Basis for Evaluation of Seismic Hazard and Design Criteria for Saudi Arabia. In Eathquake Engineering, Tenth World Conference (Vol. 10, pp. 231-258).
Aldama-Bustos, G., Bommer, J. J., Fenton, C. H., and Stafford, P. J. (2009). Probabilistic seismic hazard analysis for rock sites in the cities of Abu Dhabi, Dubai and Ra’s Al Khaymah, United Arab Emirates. Georisk: Assessment and Management of Risk for Engineered Systems and Geohazards, 3(1), 1-29.
AlHamaydeh, M., Abdalla, J., Abdalla, S., Al-Rahmani, A., and Mostafa, A. (2010). Inelastic Seismic Demands For Reinforced Concrete Frames In Dubai. In The 14th European Earthquake Engineering Conference (14EEEC), Aug. 30-Sept. 3. Ohrid, Macedonia.
AlHamaydeh, M., Abdullah, S., Hamid, A., and Mustapha, A. (2011). Seismic design factors for RC special moment resisting frames in Dubai, UAE. Earthquake Engineering and Engineering Vibration, 10(4), 495-506.
AlHamaydeh, M., and Al-Shamsi, G. (2013). Development of Analytical Fragility Curves for Representative Buildings in Dubai, United Arab Emirates. In The International Conference on Earthquake Engineering; 50 Years of European Earthquake Engineering (SE-50EEE), Skopje, Macedonia.
AlHamaydeh, M., Galal, K., and Yehia, S. (2013). Impact of lateral force-resisting system and design/construction practices on seismic performance and cost of tall buildings in Dubai, UAE. Earthquake Engineering and Engineering Vibration, 12(3), 385-397.
AlHamaydeh, M., Yehia, S., Aly, N., Douba, A., and Hamzeh, L. (2012). Design Alternatives for Lateral Force-Resisting Systems of Tall Buildings in Dubai, UAE. International Journal of Civil and Environmental Engineering, 6, 185-188.
ACI (American Concrete Institute). (2011), “Building code requirements for structural concrete and commentary.” ACI318-11, Farmington Hills, Michigan.
ASCE7/SEI (American Society of Civil Engineers/Structural Engineering Institute). (2010), “Minimum design loads for buildings and other structures.” ASCE7-10, Reston, Virginia.
ASCE41/SEI (American Society of Civil Engineers/Structural Engineering Institute). (2013). “Seismic Rehabilitation of Existing Buildings.” ASCE41-13, Reston, Virginia.
Bachmann, H., and Linde, P. (1995). Dynamic ductility demand and capacity design of earthquake-resistant reinforced concrete walls. ACI Special Publication, 157.
Baker, J. W. (2015). Efficient analytical fragility function fitting using dynamic structural analysis. Earthquake Spectra, 31(1), 579-599.
El-Sokkary, H., Galal, K., Ghorbanirenani, I., Léger, P., and Tremblay, R. (2013). Shake Table Tests on FRP-Rehabilitated RC Shear Walls. Journal of Composities for Construction, 17(1), 79-90.
ETABS. (2015). Berkeley, California: Computers and Structures Inc.
Federal Emergency Management Agency. (2010). Hazus-MH MR5 Technical Manual. Multi-hazard Loss Estimation Methodology: Earthquake Model. Washington, DC.
Federal Emergency Management Agency (FEMA). (2009). Quantification of Building Seismic Performance Factors. FEMA P695, Prepared for the Federal Emergency Management Agency, Prepared by the Applied Technology Council, Washington D.C.
Grünthal, G., Bosse, C., Sellami, S., Mayer-Rosa, D., and Giardini, D. (1999). Compilation of the GSHAP regional seismic hazard for Europe, Africa and the Middle East. Annali Di Geofisica, 42(6), 1215-1223
Humar, J., and Mahgoub, M. A. (2003). Determination of seismic design forces by equivalent static load method. Canadian Journal of Civil Engineering, 30(2), 287-307.
IBC (International Building Code). (2012), International Code Council. IBC’12, Falls Church, Virginia.
Thomsen IV, J. H., and Wallace, J. W. (2004). Displacement-Based Design of Slender Reinforced Concrete Structural Walls – Experimental Verification. Journal of Structural Engineering, 130(4), 618-630.
Khan, Z., El-emam, M., Irfan, M., and Abdalla, J. (2013). Probabilistic seismic hazard analysis and spectral accelerations for United Arab Emirates. Natural Hazards, 67, 569-589.
Krawinkler, H., and Seneviratna, G. D. P. K. (1998). Pros and cons of a pushover analysis of seismic performance evaluation. Engineering Structures, 20(4-6), 452-464.
National Center of Meteorology and Seismology of UAE. (2015). Retrieved from http://www.ncms.ae/en/
National Geosciences of Iran. (2015). Retrieved from http://www.ngdir.ir/
Panneton, M., Leger, P., and Tremblay, R. (2006). Inelastic analysis of a reinforced concrete shear wall building according to the National Building Code of Canada 2005. Canadian Journal of Civil Engineering, 33(7), 854-871.
Park, Y. J., Ang, A. H. S., and Wen, Y. K. (1987). Damage Limiting Aseismic Design of Buildings. Earthquake Spectra, 3(1), 1-26.
Pascucci, V., Free, M., and Lubkowski, Z. (2008). Seismic Hazard and Seismic Design Requirements for the Arabian Peninsula Region. In 14th World Conference on Earthquake Engineering. Beijing, China.
Quick Concrete Wall. (2015). United States of America, Bozeman: Integrated Engineering Software (IES) Inc.
M. Reinhorn, H. Roh, V. Sivaselvan, S. Kunnath, R. Valles, A. Madan, C. Li, R. Lobo, and Y. Park. (2009), “IDARC 2D Version 7.0: A Program for the Inelastic Damage Analysis of Buildings,” New York. Technical Report MCEER-09-0006, Multidisciplinary Centre for Earthquake Engineering Research, State University of New York at Buffalo.
Shama, A. (2011). Site specific probabilistic seismic hazard analysis at Dubai Creek on the west coast of UAE. Earthquake Engineering and Engineering Vibration, 10(1), 143-152.
Sigbjornsson, R., & Elnashai, A. (2006). Hazard Assessment of Dubai, United Arab Emirates, for Close and Distant Earthquakes. Journal of Earthquake Engineering, 10(5), 749-773.
Structural Engineers Association of California, S. (1999). SEAOC Blue Book, Recommended Lateral Force Requirements and Commentary (7th ed.). Sacramento, CA.
Taghavi, S., & Miranda, E. (2003). Response Assessment of Nonstructural Building Elements. Report PEER 2003/05, Pacific Earthquake Engineering Research Center, University of California, Berkeley.
Tremblay, R., Leger, P., and Tu, J. (2001). Inelastic seismic response of concrete shear walls considering P-delta effects. Canadian Journal of Civil Engineering, 24(4), 640-655.
UBC (Uniform Building Code). (1997), International Conference of Buildings Officials. UBC’97,Whittier, California.
United States Geological Survey (USGS). (2015). Retrieved May 31, 2015, from http://geohazards.usgs.gov/designmaps/ww/
Vamvatsikos, D., and Cornell, C. A. (2002). Incremental dynamic analysis. Earthquake Engineering and Structural Dynamics, 31(3), 491-514.
Vamvatsikos, D., and Cornell, C. A. (2004). Applied Incremental Dynamic Analysis. Earthquake Spectra, 20(2), 523-553.
Wallace, J. W., and Moehle, J. P. (1992). Ductility and Detailing Requirements of Bearing Wall Buildings. Journal of Structural Engineering, 118(6), 1625-1644.
[1] Associate Professor, Department of Civil Engineering, American University of Sharjah, UAE,            [email protected]
[2] Former MSc. Student, Department of Civil Engineering, American University of Sharjah, UAE; currently,  Ph.D. Student, Department of Building, Civil and Environmental Engineering, Concordia University, Montréal, Québec, Canada, [email protected]
[3] Corresponding author: Professor, Department of Building, Civil and Environmental Engineering, Concordia  University, Montréal, Québec, Canada, [email protected]