Lattice Boltzmann Method
Computational Fluid Dynamics permits the analysis of the behaviour of fluid flows in virtual environments and compared to traditional experimental tests involves lower time and costs as well as a better understanding of the studied phenomenon. Indeed, once the solution is obtai- ned all the magnitudes of the fluids can be accurately computed and visualised. Moreover, with CFD there is no interference between the flow field and the measuring equipment.
The main approach used to study the behaviour of a fluid is the continuum one, which uses the Navier-Stokes equations and describes the fluid through macroscopic properties as pressure temperature and density. Since it is difficult and time-consuming to solve directly the non-linear partial differential NS equations these are converted into a system of algebraic equations th- rough finite difference, finite volume or finite element methods. The fluid domain is discretized and each node or volume contains a huge number of particles, the average value of pressure, velocity density etc is computed through an iterative process until convergence is reached.
An alternative approach to study the fluid characteristics is the analysis of the microscale beha- viour of the fluid particles. The forces between particles (molecules) describe and determine the flow dynamic and at each time step the position and velocity of each particle is computed using the Newton’s second law of momentum conservation. From the kinetic theory macro-scale pro- perties of the fluid can be obtained. This method is clearly impractical because of the extreme number of particles that constitute even a small volume of fluid.
The LBM method is in the middle of these two methodologies and focuses the attention on di- screte collections of particles whose properties are described through a probability distribution function (PDF). The PDF describes the behaviour of a large number of particles using a sta- tistical distribution. This approach hence doesn’t request the knowledge of the single particles positions and velocities. The Maxwell-Boltzmann distribution function can be defined as the probability of finding particles within a certain range of velocities at a certain range of locations at a certain time f(r,c,t), where r,c,tare the position, velocity and time respectively.
The spatial discretization used is named lattice and it is based on a Cartesian distribution of discrete points with discrete sets of velocity directions. The lattice is determined by the number of dimensions “n” and discrete velocity directions “m” (DnQm), a large number of velocities leads to a more precise description but also a higher computational cost. For each discrete velocity direction a PDF is defined.
The Boltzmann’s Transport Equation is used to describe the evolution of the PDFs and their
interactions:
∂f
∂t+ c·∇f= Ω(f)
The equation states that the total derivative of the PDF equals to the collision operator Ω. This is a Lagrangian approach to the fluid dynamics while the traditional CFD methods use a Eulerian one. The collision operator depends on the distribution functions and it is very complicated to compute, a solution was founded by Bhatnagar, Gross and Krook (BGK) who replaced it with a single relaxation time (SRT) simplified model:
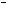
Ω = 1 (feqf)
Ï„
where feqis the local equilibrium distribution function (the distribution which represents the system equilibrium) and Ï„is the relaxation time (particle collision frequency). The above equation can be written along each velocity direction and can be discretized as
∆teq
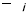fi(r+ ci∆t,t+ ∆t) = fi(r,t) +
[f (r,t)f(r,t)] Ï„i
This equation can be used to describe many phenomena specifying the proper equilibrium di- stribution function. The two steps represented are the propagation step which models the movement of the distribution functions along discrete directions and the collision step which
describes the physical phenomena.
The main drawbacks using an SRT scheme are the low Mach number which can be used, the limitations imposed by the value of Ï„and the Prandtl number must be near one.
For these reasons a multiple relaxation time (MRT) collision operator is used, this approach involves the calculation of the collision step in the momentum space instead of the velocity space.
The CFD software Xflow uses an MRT scheme which improves the stability and enhance the Mach number limitations up to Mach 0.6 for the overall fluid domain and up to Mach 1 in local regions, this means for example that a shock wave in the point of the minimum Cp value in a transonic airfoil can be captured. The lattice structure used in the software is a D3Q27 arran- ged in an octree structure. This method divides the 3D space in a tree data structure where each portion is recursively subdivided in eight equals smaller parts. In this manner, different spatial scales with different refinements can be obtained in the fluid domain. Each level has spatial and temporal scales twice as smaller than the previous one so the ratio dx/dt and the CFL condition remain constant allowing a proper time step for each node. This is an advantage towards traditional CFD method where the time step is constant and hence the calculation is inefficient for the coarse part of the mesh. Moreover, adaptive refinement criteria based on the local vorticity level can be used to refine wake regions, free surface and interfaces.
The model used to simulate subgrid turbulence is the Wall-Adapting Local Eddy (WALE) vi- scosity model. This approach is the same used for Large Eddy Simulation and introduce an artificial eddy viscosity νt. This model appears to be more efficiently applied in the LBM me- thod because the strain rate tensor is available in the local node while it needs information from the neighbours’ nodes to be evaluated in traditional CFD models. Besides, the proportional aspect ratio of the lattice required for LES turbulence model is another advantage in behalf of LBM technique.
The impossibility to represent the boundary layer near walls because of the isotropy of the latti- ce structure and the consequent high number of nodes requested to capture the phenomenon is overcome through the use of the Wall-Modeled LES approach (WMLES). Furthermore, as the turbolence length scale is proportional to the distance from the free surface and the boundary layer thickness is proportional to the Reynolds number, the resolution scale becomes unaccep- tably small near walls. This is why the WMLES approach uses RANS in the proximity of the walls.
The discrete velocities projections are also used to calculate the distance between the lattice and the geometry in order to obtain a detailed description of the body curvature which is used in WMLES to evaluate the boundary layer behaviour.