Review of Data Duplication Methods

 

Abstract: -The cloud storage services are used to store intermediate and persistent data generated from various resources including servers and IoT based networks. The outcome of such developments is that the data gets duplicated and gets replicated rapidly especially when large numbers of cloud users are working in a collaborative environment to solve large scale problems in geo-distributed networks. The data gets prone to breach of privacy and high incidence of duplication of data. When the dynamics of cloud services change over period of time, the ownership and proof of identity operations also need to change and work dynamically for high degree of security. In this work we will study the concepts; methods and the schemes that can make the cloud services secure and reduce the incident of data duplication with use of cryptography mathematics and increase potential storage capacity. The purposed scheme works for deduplication of data with arithmetic key validity operations that reduce the overhead and increase the complexity of the keys so that it is hard to break the keys.

Keywords: – De-duplication, Arithmetic validity, proof of ownership.

1. INTRODUCTION

Organizations that focus on providing online storage with strong emphasizes on the security of data based on double encryption [1] (256 bit AES or 448 bit), managed along with fish key algorithm and SSL encryption [2] based connections are in great demand. These organizations need to maintain large size data centers that have a temperature control mechanism, power backups are seismic bracing and other safeguards. But all these safeguards, monitoring and mechanism becomes expensive, if they do not take care of data duplication issues and problems related to data reduction. Data Deduplication [3] occurs especially when the setup is multi-users and the users are collaborating with each other’s work objects such as document files, video, cloud computation services and privileges etc. and volume of data grows expensively.

       In a distributed database management systems special care is taken to avoid duplication of data either by minimizing the number of writes for saving I/O bandwidth or de normalization. Databases use the concept of locking to avoid ownership issues, access conflicts and duplication issues. But even as disk storage capacities continue to increase and are becoming more cheaper, the demand for online storage has also increased many folds. Hence, the cloud service providers (CSP) continue to seek methods to reduce cost of DE-duplication and increase the potential capacity of the disk with better data management techniques. The data managers may use either compression or deduplication methods to achieve this business goal. In broad terms these technologies can be classified as data reduction techniques. The end customers are able to effectively store more data than the overall capacity of their disk storage system would allow. For example a customer has 20 TB storage array the customer may bet benefit of 5:1 which means theoretically 5 times the current storage can be availed. [(5*20 TB) = 100 TB]. The next section defines and discussed data reduction methods and issues of ownership to build trustful online storage services.

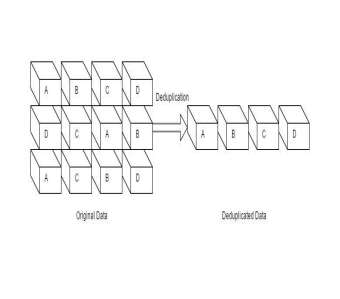
Fig: – Deduplication Process

The next section defines and discussed data reduction methods and issues of ownership to build trustful online storage services.

The purpose is to obtain a reducedrepresentation of a data set file that much smaller in volume yet provide same configure even, if the modified data in a collaborative environment. The reduced representation does not necessarily means a reduction in size of the data, but reduction in unwanted data or duplicates the existence of the data entities. In simple words the data reduction process would retain only one copy of the data and keep pointers to the unique copy if duplicates are found. Hence data storage is reduced.

Compression [4]: – It is a useful data reduction method as it helps to reduce the overall resources required to store and transmit data over network medium. However, computational resources are required for data reduction method. Such overhead can easily be offset due to the benefit it offers due to compression. However, an subject to the space time complexity trade off; for example, a video compression may require expensive investment in hardware for its compression-decompression and viewing cycle, but it may help to reduce space requirements in case there is need to achieve the video.

Deduplication [3]: – Deduplication is processed typically consist of steps that divide the data into data sets of smaller chunk sizes and use an algorithm to allocate each data block a unique hash code. In this, the deduplication process further find similarities between the previously stored hash codes to determine if the data block is already in the storage medium. Few methods use the concept comparing back up to the previous data chunks at bit level for removing obsolete data. Prominent works done in this area as follows:

1. Fuse compress – compress file system in user space.
2. Files-depot – Experiments on file deduplication.
3. Compare – A python-based deduplication command line tool and library.
4. Penknife – it's used to DE duplicate information’s in shot messages
5. Opendedup – A user space deduplication file system (SDFS)
6. Opendedupe – A deduplication based filesystem (SDFS)
7. Ostor – Data deduplication in the cloud.
8. Opensdfs – A user space deduplication file system.
9. Liten – Python based command line utility for elimination of duplicates.

Commercial:

1). Symantec

2). Comm Vault.

3). Cloud Based: Asigra, Baracuda, Jungle Disk, Mozy.

Before we engross further into this topic, let us understand the basic terms involved in the DE duplication process having in built securely features.

1. Security Keys [5]: – The security keys mainly consist of two types, namely first is “Public Key” and second is “Private Key”. The public keys are essentially cryptographic keys or sequences that can be obtained and used by anyone to encrypt data/message’s intended for particular recipient entity and can be unlocked or deciphered with the help of a key or sequence in knowledge of recipient (Private Key). Private Key is always paired with the public key and is shared only with key generator or initiator, ensuring a high degree of security and traceability.
2. Key Generation: – It is a method of creating keys in cryptography with the help of algorithms such as a symmetric key algorithm (DES or AES) and public key algorithm (such as RSA) [6]. Currently systems such as TLS [7], SSH are using computational methods of these two. The size of the keys depends upon the memory storage available on (16, 32, 64, 128 bits) etc.
3. Key Distribution: – Before, any authentication process can happen both the parties need exchange the private and public keys. In typical public key cryptography, the key distribution is done using public server keys. The key generator or initiator keeps one key to himself/herself and uploads the other key to server. In case of SSH the algorithm used is Diffie-Hellman key [6] exchange. In this arrangement, if the client does not possess a pair of public and private key along with published certificate. It is difficult for the client to proof ownership. The Figure [1] shows the life cycle of Keys used for the sake of security.

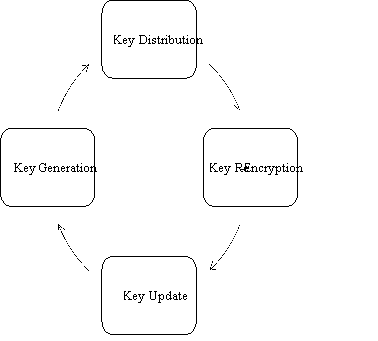
Fig 1: – Life Cycle of Key

4. Key Matching and Validation: – Since, in most cases the private key is intended to reside on the server. And, the key exchange process needs to remain secure with the use of secure shell, this is a need to have a robust key matching algorithm so that no spoofing or manipulation occur in transient. Moreover, it is always recommended that a public key validation must be done before these keys are put into operation. Public key validation tests consist of arithmetic test [8] that ensure that component of candidate informs to key generation standard. Hence, a certificate authority [9] (CA) helps in choosing the trusted parties bound by their individual identities with the help of public key. This is stated in “Certificate Produce Standards”. Some third party validators use the concept of key agreements and others may use the concept of “proof of possession” mechanism. In POP mechanism [10], for the proper establishment of keys, the user interacting is required to work with CA using a natural function of the keys (either key agreement for encryption) or by using zero-proof knowledge algorithms [11] to show possession of private key. POP shows that user owns the corresponding private key, but not necessarily, that the public key is arithmetically valid. The Public key validation (PKV) methods show that public key is arithmetically valid, but not necessary that anyone who owns the corresponding key. Combination of these (POP and PKV) methods gives a greater degree of security confidence that can be useful for Deduplication operation. However, the only issues needs to be addressed is the overhead involved in public key validation.

Improvements in arithmetic validity test can be done to improve the validation process, especially in concept of DE duplication area; where the message to be encrypted in data chunks and need to arithmetic validation and proof of ownership is to be done multiple times due to the collaborative nature of the data object. Most of the arithmetic tests validity are based on the generation and selection of prime numbers. It was in late 1989’s many people came up with an idea of solving key distribution problem for exchanging information publicly with a use of a shared or a secret cipher without someone else being able to compute the secret value. The most widely used algorithms “DiffieHellman key exchange” takes advantage of prime number series. The mathematics of prime numbers (integer whole numbers) shows that the modulus of prime numbers is useful for cryptography. The Example [Table no. 1] clearly illustrates the prime number values gets the systematically bigger and bigger, is very useful for cryptography as it has the scrambling impact. For example: –

Prime Numbers in Cryptography and Deduplication: Prime numbers [13] are whole numbers integers that have either factors 1 or same factor as itself. They are helpful in choosing disjoint sets of random numbers that do not have any common factors. With use of modular arithmetic certain large computations can be done easily with reduced number of steps. It states that remainder always remain less than divider, for example, 39 modulo 8, which is calculated as 39/7 (= 4 7/8) and take the remainder. In this case, 8 divides into 39 with a remainder of 7. Thus, 39 modulo 8 = 7. Note that the remainder (when dividing by 8) is always less than 8. Table [1] give more examples and pattern due this arithmetic.

11 modulus 8=3	17 modulus 8=1
12 modulus 8=4	18 modulus 8=2
13 modulus 8=5	19 modulus 8=3
14 modulus 8=6	20 modulus 8=4
15 modulus 8=7	21 modulus 8=5
16 modulus 8=0	So on….

       Table 1: Example of Arithmetic of modus

To do modular addition [14], two numbers are added normally, then divided by the modulus and get the remainder. Thus, (17+20) mod 7 = (37) mod 7 = 2.  The next section illustrates, how these computations are employed for cryptographic key exchange with typical example of Alice, Bod and Eva as actors in a typical scenario of keys exchange for authentication.

Step1: Sender (first person) and receiver (second person) agree, publicly, on a prime number ‘X’, having base number ‘Y’. Hacker (third person) may get public number ‘X’ access to the public prime number.

Step 2: Sender (first person) commits to a number ‘A’, as his/her “secret number exponent”. The sender keeps this secret. Receiver (second person), similarly, select his/her “secret exponent”.

Then, the first person calculates ‘Z’ using equation no. 1

Z = YA (mod X)                                    ……….. (1)

And sends ‘Z’ to Receiver (second person). Likewise, Receiver becomes calculate the value ‘C’ using equation no. 2

Z= YB (mod X)                                    ………… (2)

And sends C to Sender (first person). Note that Hacker (third person) might have both Y and C.

Step 3: Now, Sender takes the values of C, and calculate using equation no. 3

CA (mod X).                                        ………….. (3)

Step 4:  Similarly Receiver calculates using equation no. 4

ZB (mod X).                                        ………….. (4)

Step 5: The value they compute is same because K = YB (mod X) and sender computed CA (mod X) = (YB) A (mod X) = YBA (mod X). Secondly because Receiver used Z = YA (mod X), and computed ZB (mod X) = (YA) B (mod X) = YAB (mod X).

Thus, without knowing Receiver’s secret exponent, B, sender was able to calculate YAB (mod X). With this value as a key, Sender and Receiver can now start working together. But Hacker may break into the code of the communication channel by computing Y, X, Z & C just like Sender and Receiver. Experimental results in cryptography, show that it ultimately becomes a discrete algorithm problem and consequently Hacker fails to breaks the code.

The Hacker does not have any proper way to get value. This is because the value is huge, but the question is how did sender and receiver computed such a large value, it is because of modulus arithmetic. They were working on the modulus of ‘P’ and using a shortcut method called repeated squaring method. The problem of finding match to break the code for the hacker becomes a problem of discrete algorithm problem. [15]

From the above mention in this paper, it can be deduced that the athematic validity part of the security algorithm computations can also be improved by reducing number of computational steps. For this purpose Vedic mathematical methods such as [17], especially where the resources (memory to store and compute) keys are constrained.

Example: 

Base Type         Â	Example on how compute exponents using Vedic MathsÂ
If the base is taken less than 10	9^3= 9-1 / 1Ã-1 / – (1Ã-9) / 1Ã-1Ã-9 = 8 /1 / -9 / 9 = 81 / -9 / 9 = 81 – 9 / 9 = 72 / 9 = 729
If the base is taken greater  than 10	12^3= 12 + 2 / 2 Ã- 2 / + (2 Ã- 12) / 2Ã- 2 Ã- 12 = 14 / 4 / + 24 / 48 = 144 / +24 / 48 = 144 +24 / 48 = 168/ 48 = 1728

Life Cycle of Data and Deduplication:  The life cycle of digital material is normally prove to change from technological and business processes throughout their lifecycle. Reliable re-use of this digital material, is only possible. If the curation, archiving and storage systems are well-defined and functioning with minimum resource to maximum returns. Hence, control to these events in the Life Cycle is Deduplication process and securely of data.

Table: 1 recent works in key management applied in De duplication area

S. No.	Authors	Problem undertaken	Techniques  used	Goal achieved
Junbeom Hur et al. [1]	Build a secure key ownership schema that work dynamically with guaranteed data integrity against tag inconsistency attack.	Used Re-encryption techniques that enables dynamic updates upon any ownership changes in the cloud storage.	Tag consistency becomes true and key management becomes more efficient in terms of computation cost as compare to RCE (Randomized convergent encryption). However the author did not focused their work on arithmetic validity of the keys. Although the lot of work has been done on ownership of keys.
Chia-Mu Yu et al. [18]	Improve cloud server and mobile device efficiency in terms of its storage capabilities and of POW scheme.	Used improved of flow of POW with bloom filter for managing memory without the need to access disk after storing.	Reduced server side latency and user side latency.
Jorge Blasco et al. [19]	Improve the efficiency of resources (space, bandwidth, efficiency) and improve security during the DE duplication process.	Improved the working of bloom filter implementation for its usage in POW scheme and thwart a malicious client attack for colluding with the legitimate owner of the file.	Experimental resources suggest the execution time increase when size of file grows but in case of proposed scheme it helps in building a better trade off between space and bandwidth.
Jin Li et al. [20]	Build an improved key management schema that it more efficiency and secure when key distribution operation access.	The user holds an independent master key for encrypting the convergence keys and outsourcing them to could this creates lot of overhead. This is avoided by using ramp secret sharing (RSSS) and dividing the duplication phase into small phase (first and block level DE duplication).	The new key management scheme (Dekey) with help of ramp scheme reduces the overhead (encoding and decoding) better than the previous scheme.

 

Chao Yang et al. [21]	Overcome the problem of the vulnerability of client side deduplication operation, especially when the attacker try’s to access on authorized file stored on the server by just using file name and its hash value.	The concept spot checking in wheel the client only needs to access small functions of the original files dynamic do efficient and randomly chosen induces of the original file.	The proposed scheme creates better provable ownership file operation that maintains high degree of detection power in terms of probability of finding unauthorized access to files.
Xuexue Jin et al. [11]	Current methods use information computed from shared file to achieve. DE duplication of encrypted. Data or convergent encryption into method is Vulnerable as it is based well known public algorithm.	DE duplication encryption algorithm are combined with proof of ownership algorithm to achieve higher degree of security during the DE duplication  process. The process is also argument with proxy re-encryption (PRE) and digitalize credentials checks.	The author achieved anonymous DE duplication encryption along with POW test, consequently the level of protection was increased and attacks were avoided.
Danny Harnik et al. [22]	Improve cross user (s) interaction securely with higher degree of privacy during DE duplication.	The authors have described multiple methods that include:- (a). Stop cross over user interaction. (b). Allow user to use their own private keys to encrypt. (c). Randomized algorithm.	Reduced the cost of operation to secure the duplication process. Reduced leakage of information during DE duplication process. Higher degree of fortification.
Jingwei Li et al. [23]	The authors have worked on the problem of integrity auditing and security of DE duplication.	The authors have proposed and implemented two methods via Sec Cloud and Sec Cloud+, both systems improve auditing the maintain ace with help of map reduce architecture.	The Implementation provided performance of periodic integrity check and verification without the local copy of data files. Better degree of proof of ownership process integrated with auditing.
Kun He et al. [24]	Reduce complications due to structure diversity and private tag generation. Find better alternative to homomorphic authenticated tree. (HAT)	Use random oracle model to avoid occurrence of breach and constructs to do unlimited number of verifications and update operations. DeyPoS which means DE duplicable dynamic proof of storage.	The theoretical and experimental results show that the algorithm (DeyPoS) implementation is highly efficient in conditions where the file size grows exponentially and large number of blocks are there.
Jin Li et al. [25]	The provide better protected data, and reduce duplication copies in storage with help of encryption and alternate Deduplication method.	Use hybrid cloud architecture for higher degree of security (taken based) , the token are used to maintain storage that does not have Deduplication and it is more secure due to its dynamic behavior.	The results claimed in the paper shows that the implemented algorithm gives minimal overhead compared to the normal operations.
Zheng Yan et al. [26]	Reduce the complexity of key management step during data duplication process	But implement less complex encryption with same or better level of security. This is done with the help of Attribute Based Encryption algorithm.	Reduce complexity overhead and execution time when file size grows as compared to preview work.

Summary of Key Challenges Found

1. The degree of issues related to implementation of Crypto Algorithms in terms of mathematics is not that difficult as compared to embracing and applying to current technological scenarios.
2. Decentralized Anonymous Credentials validity and arithmetic validity is need to the hour and human sensitivity to remain safe is critical.
3. In certain cases, the need to eliminate a trusted credential issuers can help to reduce the overhead without compromising the security level whole running deduplication process.
4. Many algorithms for exponentiation do not provide defense against side-channel attacks, when deduplication process is run over network. An attacker observing the sequence of squaring and multiplications can (partially) recover the exponent involved in the computation.
5. Many methods compute the secret key based on Recursive method, which have more overhead    as compared methods that are vectorized. Some of the vectorized implementations of such   algorithms can be improved by reducing the number of steps with one line computational methods, especially when the powers of exponent are smaller than 8.
6. There is a scope of improvement in reducing computational overhead in methods of computations of arithmetic validity methods by using methods such as Nikhilam Sutra, Karatsuba.

CONCLUSION

In this paper, sections have been dedicated to the discussion on the values concepts that need to be understood to overcome the challenges in De-duplication algorithms implementations. It was found that at each level of duplication process (file and block) there is a needs for keys to be arithmetically valid and there ownership also need proved for proper working of a secure duplication system. The process becomes prone to attacks, when the process is applied in geo-distributed storage architecture.  The complexity for cheating ownership verification is at least difficult as performing strong collision attack of the hash function due to these mathematical functions.  Finding the discrete algorithm of a random elliptic curve element with respect to a publicly known base point is infeasible this is (ECDLP). The security of the elliptic curve cryptography depends on the ability to the compute a point multiplication and the mobility to compute the multiple given the original and product points. The size of the elliptic curve determines the difficulty of the problem.

FUTURE SCOPE

As discussed, in the section mathematical methods such as Nikhilam Sutra, Karatsuba Algorithm [27] may be used for doing computations related to arithmetic validity of the keys produced for security purpose as it involves easier steps and reduce the number of bits required for doing multiplication operations etc. Other than this, the future research work to apply to security network need of sensors that have low memory and computational power to run expensive cryptography operations such public key validation and key exchange thereafter.

[1]	J. Hur, D. Koo, Y. Shin and K. Kang, “Secure data deduplication with dynamic ownership management in cloud storage,” IEEE Transactions on Knowledge and Data Engineering, vol. 28, pp. 3113–3125, 2016.

1. A. Kumar and A. Kumar, “A palmprint-based cryptosystem using double encryption,” in SPIE Defense and Security Symposium, 2008, pp. 69440D–69440D.
2. M. Portolani, M. Arregoces, D. W. Chang, N. A. Bagepalli and S. Testa, “System for SSL re-encryption after load balance,” 2010.
3. W. Xia, H. Jiang, D. Feng, F. Douglis, P. Shialane, Y. Hua, M. Fu, Y. Zhang and Y. Zhou, “A comprehensive study of the past, present, and future of data deduplication,” Proceedings of the IEEE, vol. 104, pp. 1681-1710, 2016.
4. J. Ziv and A. Lempel, “A universal algorithm for sequential data compression,” IEEE Transactions on information theory, vol. 23, pp. 337–343, 1977.
5. P. Kumar, M.-L. Liu, R. Vijayshankar and P. Martin, “Systems, methods, and computer program products for supporting multiple contactless applications using different security keys,” 2011.
6. S. Gupta, A. Goyal and B. Bhushan, “Information hiding using least significant bit steganography and cryptography,” International Journal of Modern Education and Computer Science, vol. 4, p. 27, 2012.
7. K. V. K. and A. R. K. P. , “Taxonomy of SSL/TLS Attacks,” International Journal of Computer Network and Information Security, vol. 8, p. 15, 2016.
8. J. M. Sundet, D. G. Barlaug and T. M. Torjussen, “The end of the Flynn effect?: A study of secular trends in mean intelligence test scores of Norwegian conscripts during half a century,” Intelligence, vol. 32, pp. 349-362, 2004.
9. W. Lawrence and S. Sankaranarayanan, “Application of Biometric security in agent based hotel booking system-android environment,” International Journal of Information Engineering and Electronic Business, vol. 4, p. 64, 2012.
10. N. Asokan, V. Niemi and P. Laitinen, “On the usefulness of proof-of-possession,” in Proceedings of the 2nd Annual PKI Research Workshop, 2003, pp. 122–127.
11. X. Jin, L. Wei, M. Yu, N. Yu and J. Sun, “Anonymous deduplication of encrypted data with proof of ownership in cloud storage,” in Communications in China (ICCC), 2013 IEEE/CIC International Conference on, 2013, pp. 224–229.
12. D. Whitfield and M. E. Hellman, “New directions in cryptography,” IEEE transactions on Information Theory, vol. 22, pp. 644–654, 1976.
13. H. Riesel, “Prime numbers and computer methods for factorization,” vol. 126, Springer Science & Business Media, 2012.
14. R. A. Patel, M. Benaissa, N. Powell and S. Boussakta, “Novel power-delay-area-efficient approach to generic modular addition,” IEEE Transactions on Circuits and Systems I: Regular Papers, vol. 54, pp. 1279–1292, 2007.
15. “Repeated Squaring,” Wednesday March 2017. [Online]. Available:

http://www.algorithmist.com/index.php/Repeated_Squaring. [Accessed Wednesday March 2017].

16. “Table of costs of operations in elliptic curves,” Wednesday March 2017. [Online]. Available:

https://en.wikipedia.org/wiki/Table_of_costs_of_operations_in_elliptic_curves. [Accessed Wednesday March 2017].

17. “Calculating Powers Near a Base Number,” Wednesday March 2017. [Online]. Available:

http://www.vedicmaths.com/18-calculating-powers-near-a-base-number. [Accessed Wednesday March 2017].

18. C.-M. Yu, C.-Y. Chen and H.-C. Chao, “Proof of ownership in deduplicated cloud storage with mobile device efficiency,” IEEE Network, vol. 29, pp. 51–55, 2015.
19. J. Blasco, R. D. Pietro, A. Orfila and A. Sorniotti, “A tunable proof of ownership scheme for deduplication using bloom filters,” in Communications and Network Security (CNS), 2014 IEEE Conference on, 2014, pp. 481–489.
20. J. Li, X. Chen, M. Li, J. Li, P. P. Lee and W. Lou, “Secure deduplication with efficient and reliable convergent key management,” IEEE transactions on parallel and distributed systems, vol. 25, pp. 1615–1625, 2014.
21. C. Yang, J. Ren and J. Ma, “Provable ownership of files in deduplication cloud storage,” Security and Communication Networks, vol. 8, pp. 2457–2468, 2015.
22. D. Harnik, B. Pinkas and A. Shulman-Peleg, “Side channels in cloud services: Deduplication in cloud storage,” IEEE Security & Privacy, vol. 8, pp. 40–47, 2010.
23. J. Li, J. Li, D. Xie and Z. Cai, “Secure auditing and deduplicating data in cloud,” IEEE Transactions on Computers, vol. 65, pp. 2386–2396, 2016.
24. K. He, J. Chen, R. Du, Q. Wu, G. Xue and X. Zhang, “Deypos: deduplicatable dynamic proof of storage for multi-user environments,” IEEE Transactions on Computers, vol. 65, pp. 3631–3645, 2016.
25. J. Li, Y. K. Li, X. Chen, P. P. Lee and W. Lou, “A hybrid cloud approach for secure authorized deduplication,” IEEE Transactions on Parallel and Distributed Systems, vol. 26, pp. 1206–1216, 2015.
26. Z. Yan, M. Wang, Y. Li and A. V. Vasilakos, “Encrypted data management with deduplication in cloud computing,” IEEE Cloud Computing, vol. 3, pp. 28–35, 2016.
27. S. P. Dwivedi, “An efficient multiplication algorithm using Nikhilam method,” 2013.