Review of Optimal PMU Placement Methods

Abstract-The Phasor Measurement Unit (PMU) is very important tool for monitoring and control of the power system. PMUs give real time, synchronized measurements of voltages at the buses and also current phase values which are incident to those buses where these PMUs are located. It is unnecessary and impossible to place PMU at each bus to estimate the states because the PMUs and communication facilities are very costly. It is necessary to determine the minimum number of PMUs for entire observability of the power network. The optimal placement of PMUs (OPP) problem solved by various techniques such as mathematical programming, metaheuristic techniques. A literature review on these technologies to solve OPP problem is proposed in this paper.

I. INTRODUCTION

At present due to increased power demand, fast growth of generation, transmission, and development in power systems congested the existing networks and therefore stability margin of these networks are decreased. In this situation to make sure proper and stable operation of the power system, an accurate measurement and system states monitoring is required. This was normally done by Supervisory Control and Data Acquisition (SCADA) system, where system states estimation depends on unsynchronized measurement[1]. These measurements have errors such as measurement and telemetry bias. To overcome these limitations in the SCADA, Wide Area Monitoring Protection and Control (WAMPAC) system is used[2]. This system consist Phasor Measurement Units (PMUs) as fundamental components which give synchronized and real-time voltages and currents phasor measurement[3]. Global Positioning System Satellite (GPS) provides reference timing signals to achieve synchronization of sampling voltage and current waveform with respect to this reference time. A PMU directly measures the voltage Phase of the bus where these PMUs are placed and also measure the current phases of a few or all the branches connected to that bus. In recent years to improve monitoring use of PMUs are rapidly increases, so it needs to place these PMUs on all of the buses for full observability of the network. It is also impossible to place these units on entire system buses because PMUs and communication services are very costly[4]. Thus determination of the optimal number of PMUs and its location for overall observability of the system is very important.

A proper methodology is required to find the optimum number of the PMUs which will fully observe the power network. To solve the Optimal PMUs Placement (OPP) problem a number of methods have been employed[5]. These methods usually classified into conventional methods and advanced heuristic and modern metaheuristic methods[6] : Linear Programming, Nonlinear Programming, Dynamic Programming are the common optimization methodologies are proposed to solve this problem. Problems such as difficulties of obtaining local minima and handling constraints in conventional techniques are overcome by advanced heuristic and modern metaheuristic optimization methodology. These methodologies are Depth First Search, Minimum Spanning Tree, Simulated Annealing, Tabu Search, Genetic Algorithms, Differential Evaluation, Immune Algorithms, Partical Swarm Optimization or Ant Colony Optimization [7]. This paper reviews the research work and studies that have been done in the area of optimal placement of phasor measurement units (PMUs). Mainly the conventional and recent advanced heuristic and metaheuristic optimization techniques are presented in this paper to solve the typical optimal placement of PMUs problem. The formulation of this problem is described in Section II.The new methods to solve the OPP problem are discussed in Sections III and IV. Section V concludes this paper.

II. OPTIMAL PMU PLACEMENT (OPP) PROBLEM FORMULATION

PMU is an intelligent device which measures the phase value of voltage and current of bus which are connected to it.

Figure 1 shows PMUs which purely isolated form a Wide Area Monitoring System (WAMS).GPS time stamped measurement signals are fed to a Phasor Data Concentrator (PDC) by using PMUs. The PDC collects and sorts the phasor measurements and signal processor converts data of PMUs into useful information which is visible on Human Machine Interface (HMI).The operator can easily access the critical information of the power system state. Some rules can be used for the placement of PMUs which are given in [8] like, assigning one voltage measurement at the bus where PMU is located, one branch current measurement, one voltage and current pseudo measurement.

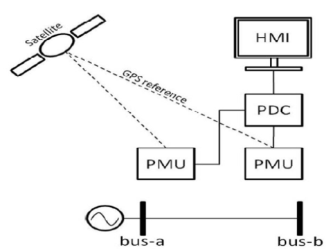
Figure 1.Layout of PMU along with GPS time stamped signals

The PMUs can be placed at planned buses to completely observe the total network. These located PMUs are measuring the voltage phase value of that bus and current phase values of the lines which are connected to the same bus. The aim is to completely observe the network with an optimum number of PMUs. The problem for n-bus system is formulated and solved by Integer Programming method [6]as given below:

Min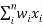

Subject to f(x)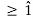

Where x = binary decision variable vector,

.

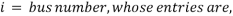
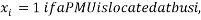
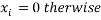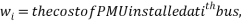
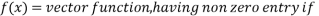
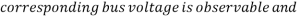
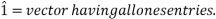
The nonlinear constraint expressions are created considering the placement and types of available measurements. Assume the phasor value of voltage at the bus where PMU located and values of current phasors along the branches which connected to that bus will be easily accessible. The other adjacent bus voltages will also be accessible. Determine the solution vector which is a set of minimum and satisfy above equation. The constraint function can be defined with the help of Binary Connectivity Matrix A which gives the information about bus connectivity of power network. The elements of matrix A is defined as,

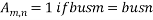
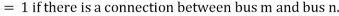
= 0 otherwise.

The constraint equations are considered for the three cases: (1) PMU measurements only, (2) PMU measurements and injections (i.e. zero injections) and (3) PMU measurements, injections, and flows.

Different formulations of the PMU placement problem with additional constraints have been presented in the literature, Effects of Zero Injection Buses[9], Effect of conventional measurements[10], single or multiple PMU loss contingency[11], single branch outage[12], contingency of single line outage or single PMU loss[13], effect of PMU channel limit[14].

III. MATHEMATICAL PROGRAMMING METHODS

Integer Programming (IP) is a numerical programming method it also known as mathematical programing. It solves an optimization problem which has integer design variables. According to reference [15], whether they are linear, nonlinear or quadratic, an integer programming is divided into Integer Linear Programming (ILP), Integer Nonlinear Programming (INLP) and Integer Quadratic Programming (IQP) respectively.

This paper gives the implementation of Integer Linear Programming (ILP) for optimal PMU placement for full power system observability. Modeling of zero injection constraints in ILP frame work has given. A method has been proposed to the systems having zero injection busses in which we use binary connectivity matrix modification and the modified matrix can be used in Integer Linear programming (ILP) for optimal PMU placement. ILP approach has also been given for the systems considering single PMU outage. The results specify that: 1) optimal PMU placement for full power system observability can be computed effectively; 2) connectivity matrix modification based approach for systems having zero injection buses is computationally efficient and easy to execute; 3) number of PMUs has to increase for systems considering single PMU outage. The proposed algorithms have been tested for IEEE – 9 bus, IEEE – 14 bus, IEEE – 24 bus test systems on MATLAB environment [16].

This paper presents a unified binary semidefinite programming (BSDP) model with binary decision variables, for optimal placement of phasor measurement units, considering the impact of pre-existing conventional and synchronized phasor measurements as well as the limited channel capacity of phasor measurement units. A linear objective function is minimized subject to linear matrix inequality observability constraints. The developed method is solved with an outer approximation scheme based on binary integer linear programming. The proposed method is illustrated using the IEEE 14-bus test system. Simulations are conducted on the IEEE 57-bus and 118-bus test systems to prove the validity of the proposed method [17].

For the observability of system, an Integer Linear Programming (ILP) method is used. It also reduces the number of PMUs and maximizes the measurement redundancy in the power system buses. This paper utilizes two approaches, Newton Raphson method and Weight Least Squares (WLS) state estimation method for estimating voltage magnitude and phase angles at each bus. The true value obtained from NR method is compared with the estimated values obtained from WLS with and without the inclusion of PMU measurements. The employed techniques are tested on IEEE- 14 and 30 bus system for determining the optimal points of placement of PMUs to measure the accurate voltage magnitude and phase angle at each bus [18].

We define the desired solution as the PMU placement that also achieves best overall state estimation performance. Accordingly, we derive the state estimator of all buses in a three-phase network and propose a) greedy algorithm and b) integer programming optimization method to determine the optimal solution. The comparative performance of these two methods is presented via evaluation of transmission and distribution test networks [19].

This paper aims to optimize the PMU (Phasor Measurement Unit) placement for a full observation of the power network and the minimum number of PMUs. In this paper competition of Mixed Integer Non-Linear Programming and heuristically algorithms such as Bacterial Foraging Algorithm was presented. The results are demonstrated with PMU placement optimization simulation and a redundancy measurement analysis by using IEEE14-bus and Tehran Regional electric company 41-bus networks [20].

This paper presents a method for the use of synchronized measurements for complete observability of a power system. The placement of phasor measurement units (PMUs), utilizing time-synchronized measurements of voltage and current phasors, is studied in this paper. An integer quadratic programming approach is used to minimize the total number of PMUs required, and to maximize the measurement redundancy at the power system buses. Existing conventional measurements can also be accommodated in the proposed PMU placement method. Complete observability of the system is ensured under normal operating conditions as well as under the outage of a single transmission line or a single PMU. Simulation results on the IEEE 14-bus, 30-bus, 57-bus, and 118-bus test systems as well as on a 298-bus test system are presented in this paper [21].

B. Exhaustive Search

Exhaustive search is a general optimization technique that systematically enumerates all possible candidates for the solution and selects the candidate that satisfies the constraints at the optimum value of the objective function. Its main advantage is that it guarantees the finding of the global optimum. However, it is not suitable for large-scale systems with huge search space.

Observability of bulk power transmission network by means of a minimum number of phasor measurement units (PMUs), with the aid of the network topology, is a great challenge. This paper presents a novel equivalent integer linear programming method (EILPM) for the exhaustive search-based PMU placement. The state estimation implemented based on such a placement is completely linear, thereby eliminating drawbacks of the conventional SCADA-based state estimation. Additional constraints for observability preservation following single PMU or line outages can easily be implemented in the proposed EILPM. Furthermore, the limitation of communication channels is dealt with by translation of nonlinear terms into linear ones. Optimal PMU placement is carried out on the IEEE 118-bus test system in different scenarios. The comparison between obtained results of EILPM and those of other methods reveals optimality of the solutions. Moreover, the proposed method is successfully applied on the Iranian National Grid, which demonstrates it can effectively be employed for practical power networks [22].

This paper gives Exhaustive Search (ES) algorithms for optimal PMU placement for full power system observability. The results specify that: 1) optimal PMU placement for full power system observability can be computed effectively; 2) connectivity matrix modification based approach for systems having zero injection buses is computationally efficient and easy to execute; 3) number of PMUs has to increase for systems considering single PMU outage. The proposed algorithms have been tested for IEEE – 9 bus, IEEE – 14 bus, IEEE – 24 bus test systems onMATLAB environment [16].

This paper presents a unified binary semidefinite programming (BSDP) model with binary decision variables, for optimal placement of phasor measurement units, considering the impact of pre-existing conventional and synchronized phasor measurements as well as the limited channel capacity of phasor measurement units. A linear objective function is minimized subject to linear matrix inequality observability constraints. The developed method is solved with an outer approximation scheme based on binary integer linear programming. The proposed method is illustrated using the IEEE 14-bus test system. Simulations are conducted on the IEEE 57-bus and 118-bus test systems to prove the validity of the proposed method [17].

IV. HEURISTIC ALGORITHMS

A. Genetic Algorithm (GA)

Genetic algorithm (GA) is adaptive heuristic search algorithm that repeats the process of natural evolution. This process is used to generate solutions to optimization and also search problem, The utilization of Genetic Algorithms (GA) in tackling engineering problems has been a major issue arousing the curiosity of researchers and practitioners in the area of systems and engineering research, operations research and management sciences in the past decades are described in [23].

This paper models genetic algorithm into the Map Reduce model, so the MapReduce genetic algorithm (MRGA) possesses some parallel computing performance, such as scalability, better fitness convergence and so on. MRGA is implemented on computing clusters of Hadoop to search the optimal configuration of PMU. Meanwhile, this feasibility and the computing performance of MRGA is verified by the IEEE14-node system, IEEE118-node system, and Wp2383-node system. This method has significant advantages in the installed PMU number, the diversity of solution, the astringency and the practicability [24].

B. Tabu Search (TS)

This paper introduces a recursive Tabu search (RTS) method to solve the OPP problem. More specifically, the traditional Tabu search (TS) metaheuristic algorithm is executed multiple times, while in the initialisation of each TS the best solution found from all previous executions is used. The proposed RTS is found to be the best among three alternative TS initialisation schemes, in regard to the impact on the success rate of the algorithm. A numerical method is proposed for checking network observability, unlike most existing metaheuristic OPP methods, which are based on topological observability methods. The proposed RTS method is tested on the IEEE 14, 30, 57 and 118-bus test systems, on the New England 39-bus test system and on the 2383-bus power system. The obtained results are compared with other reported PMU placement methods. The simulation results show that the proposed RTS method finds the minimum number of PMUs, unlike earlier methods which may find either the same or even higher number of PMUs [25].

The contribution of this paper is as follows: at first, analyze the measurement placement design of the electric power system using the software PSAT. Second, the heuristic approach, Tabu search (TS), based on topological analysis is proposed to solve the problem. The heuristic algorithm uses augmented incidence matrix to focus on the power system state estimator model then an Optimal PMU Placement (OPP) problem is formulated for the configuration with the minimum number of measurements that satisfies the observability constraints. Tests on the IEEE 14-Bus system and the TN are used to demonstrate the validity, flexibility, and efficiency of the proposed approach [26].

C. Simulated Annealing (SA)

This paper proposes a two-step optimization approach for optimal placement of phasor measurement unit (PMU) to obtain complete observability of power system in the case of preinstalled PMUs. The complete observability of the system in the case of normal operation and pre-installed PMUs is formulated and then, different contingency conditions in the system are considered, i.e. single line outage and single bus outage. At the first step of the proposed two-step optimization approach, a minimization model is applied to convex programing (cvx) to achieve the minimum number of PMUs which guarantees the complete observability of the system. At the second step, simulated annealing (SA) is applied to maximize the measurement redundancy. Additionally, to further reduce the number of required PMUs the zero-injection bus effect is considered. At last, the proposed approach is tested on several IEEE standard systems, i.e. IEEE 14-bus, 30-bus, 39-bus, IEEE 16-machine 68-bus and 118-bus, to demonstrate the effectiveness of the proposed approach [13].

This paper presents a novel Multi-Stage Simulated Annealing algorithm for the joint placement of PMUs along with the existing conventional measurement units in the power grid network. The proposed multi-stage optimization method enables Simulated Annealing to reach the optimal point faster than conventional Simulated Annealing methods. The controlled uphill movements during various stages facilitate to obtain best possible solution [27].

D. Differential Evolution (DE)

In this paper, differential evolution (DE) algorithm has been proposed to solve an optimal joint placement problem of phasor measurement units (PMUs) and conventional measurements which enable to determine the state variables of the power system. The problem is to minimize the number of PMUs required for network observability and to maximize the PMU measurements redundancy. This is achieved by selecting a solution with maximum System Observability Redundancy Index (SORI) if multiple optimal solutions exist. The resulting nonlinear integer programming (NLIP) problem is solved by the proposed DE method for the optimal solution by considering different power system problems viz. a 7-bus test and IEEE 14-bus systems with and without the consideration of zero injection buses. Results thus obtained have also been validated with existing solution techniques [28].

E. Particle Swarm Optimization (PSO)

An exponential binary particle swarm optimization (EBPSO) algorithm is proposed to solve the OPP problem for a completely observable network. Various practical contingencies such as zero injection, single PMU outage are considered in the proposed algorithm along with the normal operating condition. Multiple solutions for OPP problem can improve the feasibility of the placement methodology in a practical environment. Even though any bus is selected as candidate location but it may not be possible to install a PMU on that bus due to the lack of necessary infrastructure. On the contrary, few buses in practical systems which require close and precise monitoring should be directly observed by PMU. Placing some extra PMUs can solve this problem but economically it is not preferable. Hence, having alternative solutions can be very effective. To ensure multiple solutions and improve the performances, an adaptive exponentially decaying inertia weight coefficient is developed. A sigmoid function is introduced to update the position of the particles in binary form. Both inter connected (IEEE 14-bus and 30-bus) and radial (IEEE 39-bus) system are tested to check the feasibility and effectiveness of the algorithm [29].

This paper proposes a Particle Swarm Optimization based method to find the optimal PMU locations in a given grid topology. This method was tested successfully with the IEEE 14-bus, 30-bus, and 68-bus systems as well as with a large portion of the Brazilian power system [30].

This paper presents an Improved PSO Algorithm (IPSO) to solve the problem of optimal Phasor Measurement Unit (PMU) placement. The aim of Optimal PMU Placement problem is to guarantee both full observabilities of the power grid and minimal number of PMU. In the Improved PSO Algorithm, the point of genetic algorithm and the simulated annealing process is involved into basic particle swarm optimization. To deal with the constraints, an improved Algorithm is developed and it can avoid costing much time and trapping local optimal solution. IEEE systems are tested to show the feasibility and effectiveness of the algorithm [31].

F. Immune Algorithm (IA)

G. Iterated Local Search (ILS)

The objective of the paper is to minimise the size of the PMU configuration while allowing full observability of the network. The method proposed initially suggests a PMU distribution which makes the network observable. The Iterated Local Search (ILS) metaheuristic is then used to minimise the size of the PMU configuration needed to observe the network. The algorithm is tested on IEEE test networks with 14, 57 and 118 nodes and compared to the results obtained in previous publications [32].

H. Spanning Tree Search

The objective is to use the spanning tree approach and tree search technique for optimal placement of multichannel and minimum channel synchronized phasor measurement units (PMUs) in order to have full observability of Power System. The novel concept of depth of observability is used and its impact on the number of PMU placements is explained. The spanning tree approach is used for the power system graphs and a tree search technique is used for finding the optimal location of PMUs. This is tested on IEEE-14 and IEEE-30 bus system. The same technique is modified to optimally place minimum channel PMUs on the same IEEE-14 and IEEE-30 bus systems. Matlab tool has been used for fulfilling the objective [33].

I. Greedy Algorithm

Paper [34] propose a greedy PMU placement algorithm and show that it achieves an approximation ratio of (1-1/e) for any PMU placement budget. We further show that the performance is the best that one can achieve, in the sense that it is NP-hard to achieve any approximation ratio beyond (1-1/e). Such performance guarantee makes the greedy algorithm very attractive in the practical scenario of multi-stage installations for utilities with limited budgets. Finally, simulation results demonstrate the near-optimal performance of the proposed PMU placement algorithm.

This paper studies the placement problem of PMUs in distribution system considering the system reconfiguration. System reconfiguration is achieved using the ant colony optimization method to solve the minimum power losses problem. A Greedy algorithm is used as an optimization tool to determine the minimal number of PMUs and their locations. The 33-bus distribution system is studied for optimal installation of PMUs with different distribution network topologies [35].

J. Recursive Security Algorithm

The recursive security algorithm is a spanning tree search of multiple solutions, with a different starting point.

Recursive spanning tree algorithm of PSAT is applied to find out the minimal placement locations for observability of all buses. The Thevenin’s equivalent parameters have been obtained from the measured and estimated voltages at the load buses and impedance matrix Zbus. The parameters obtained are used to find the voltage stability boundary. Results on the IEEE-14 bus system and IEEE-30 bus system are presented to illustrate the proposed approach [36].

K. Teaching-Learning-Based optimization Algorithm

In this paper, Teaching-Learning-Based optimization Algorithm (TLBO) is presented for solving the problem of placement of PMU optimally in a power system network for complete observability. The TLBO algorithm enables optimal PMU placement by zero injection measurements and also by not including zero injection measurements. The algorithm has been tested on standard test systems such as IEEE 14-bus, IEEE 30-bus, IEEE 57-bus and the results are contrasted with other optimization algorithms like Genetic Algorithm and Binary PSO [37].

L. Improved binary particle swarm

This paper presents the improved binary particle swarm (IBPSO) method that converges faster and also manage to maximize the measurement redundancy compared to the existing BPSO method. This method is applied to IEEE-30 bus system for the case of considering zero-injection bus and its effectiveness is verified by the simulation results done by using MATLAB software [38].

M. Best first search (BFS) algorithm

This paper utilizes best first search (BFS) algorithm to determine the optimal placement of PMUs for complete observability of a power system under normal operating conditions. The additional redundancy offered by this method has been removed by applying a pruning technique to further minimize the number of PMUs determined by BFS algorithm. The proposed method has been used to determine the optimal PMU placement solutions for the standard IEEE 14-bus system, IEEE 30-bus system and a practical 246-bus Indian system. The results obtained with the proposed method have been compared with the existing methods such as integer linear programming. It has been found that the proposed method is able to achieve the complete system observability with the minimum number of PMUs required [39].

N. Mixed heuristic/matheuristic method

This paper presents a new method for the optimal allocation of PMUs in substations with a focus on the two-level state estimation process that was recently proposed in the specialized literature. A mixed heuristic/matheuristic method is proposed to determine the number and location of those units in such a way to provide robust observability characteristics. Its reliable, robust, and precise results are shown for small and large substation layouts [40].

O. Measurement sensitivity analysis

This article presents a novel algorithm to find optimal sets of Phasor Measurement Units (PMUs) in power systems using measurement sensitivity analysis aiming for fault detection without multi-estimation. The algorithm generalizes the impedance method in fault detection through optimizing PMU utilization in order to detect a fault with desired precision in interconnected power systems. By deriving bus voltage and currents sensitivity indices to the fault location and impedance, possible deviations of the estimated fault location and/or impedance due to measurement noise, accuracy, precision limits, or simply the inability of a measurement point to sense a fault is evaluated. Therefore, the algorithm can solve Optimal PMU Placement (OPP) for desired fault detection precision based on these indices for various points of measurement observing faults in the system. Finally, avoiding multi-estimation guarantees the unique mapping between measurements of the selected PMU sets and faults throughout the system. The proposed algorithm is performed on the IEEE 7-bus and 14-bus benchmark systems and the fault location capability is evaluated through neural networks [41].

P. Modified binary cuckoo optimization algorithm

In this study, a new evolutionary algorithm named as modified binary cuckoo optimization algorithm (MBCOA) is presented to solve optimal PMU placement (OPP) problem. The proposed method is classified as topological approaches. The basis of the method is in the lifestyle of the brood parasite bird named cuckoo that immigrates to the best habitat to obtain sufficient food and suitable nests for egg laying. The proposed binary structure is not introduced and applied to OPP problem up to now. OPP is tested on different networks consist of IEEE 14, 30, 57 and 118 bus test systems during normal operation and single event contingencies, i.e. single PMU failure and single line outage. The proposed MBCOA is also applied to 2383 and 2746 bus test systems to show its ability to handle large scale power networks. It is shown that MBCOA can obtain the best result from the search region with a minimum number of iterations [42].

References:

[1]M. A. Rahman, A. H. M. Jakaria, and E. Al-shaer, “Formal Analysis for Dependable Supervisory Control and Data Acquisition in Smart Grids,” in 2016 46th Annual IEEE/IFIP International Conference on Dependable Systems and Networks (DSN), 2016, pp. 263-274.

[2]Jiaping Liao and Cheng He, “Wide-area monitoring protection and control of future power system networks,” in 2014 IEEE Workshop on Advanced Research and Technology in Industry Applications (WARTIA), 2014, pp. 903-905.

[3]M. Wache, “Application of phasor measurement units in distribution networks,” in 22nd International Conference and Exhibition on Electricity Distribution (CIRED 2013), 2013, pp. 0498-0498.

[4]A. Pal, A. K. S. Vullikanti, and S. S. Ravi, “A PMU Placement Scheme Considering Realistic Costs and Modern Trends in Relaying,” IEEE Trans. Power Syst., pp. 1-1, 2016.

[5]J. Paudel, Xufeng Xu, and E. B. Makram, “PMU deployment approach for maximum observability considering its potential loss,” in 2016 IEEE/PES Transmission and Distribution Conference and Exposition (T&D), 2016, pp. 1-5.

[6]K. K. More and H. T. Jadhav, “A literature review on optimal placement of phasor measurement units,” 2013 Int. Conf. Power, Energy Control, pp. 220-224, Feb. 2013.

[7]N. M. Manousakis, G. N. Korres, and P. S. Georgilakis, “Optimal placement of phasor measurement units: A literature review,” in 2011 16th International Conference on Intelligent System Applications to Power Systems, 2011, pp. 1-6.

[8]V. V. R. Raju and S. V. J. Kumar, “An optimal PMU placement method for power system observability,” in 2016 IEEE Power and Energy Conference at Illinois (PECI), 2016, pp. 1-5.

[9]K. Gharani Khajeh, E. Bashar, A. Mahboub Rad, and G. B. Gharehpetian, “Integrated Model Considering Effects of Zero Injection Buses and Conventional Measurements on Optimal PMU Placement,” IEEE Trans. Smart Grid, pp. 1-1, 2015.

[10]R. Kavasseri and S. K. Srinivasan, “Joint optimal placement of PMU and conventional measurements in power systems,” in Proceedings of 2010 IEEE International Symposium on Circuits and Systems, 2010, pp. 3449-3452.

[11]S. M. Mazhari, H. Monsef, H. Lesani, and A. Fereidunian, “A multi-objective PMU placement method considering measurement redundancy and observability value under contingencies,” IEEE Trans. Power Syst., vol. 28, no. 3, pp. 2136-2146, Aug. 2013.

[12]N. Manousakis and G. Korres, “Optimal Allocation of PMUs in the Presence of Conventional Measurements Considering Contingencies,” IEEE Trans. Power Deliv., pp. 1-1, 2016.

[13]S. Akhlaghi, “Optimal PMU placement considering contingency-constraints for power system observability and measurement redundancy,” in 2016 IEEE Power and Energy Conference at Illinois (PECI), 2016, pp. 1-7.

[14]V. Rokkamand and R. Bhimasingu, “A novel approach for optimal PMU placement considering channel limit,” in 2014 International Conference on Power System Technology, 2014, pp. 1164-1171.

[15]E. Castillo, A. J.Conejo, P. Pedregal, R. Garciá, and A. Natalia, Building and Solving Mathematical Programming Models in Engineenng and Science. Wiley, 2002.

[16]R. R. Researchers, M. Energy, S. Phdvxuhphqwv, I. Duh, X. Lq, F. Zlwk, S. O. H. Ydoxhv, R. I. Yrowdjhv, and D. W. Qrghv, ” ‘ HWHFWLRQ RI 6 VWHPDWLF ( UURUV LQ 308 0HDVXUHPHQWV E WKH 3RZHU 6 VWHP 6WDWH ( VWLPDWLRQ 0HWKRGV,” vol. 7, pp. 7-10.

[17]N. M. Manousakis, G. N. Korres, and S. Member, “Semidefinite Programming for Optimal Placement of PMUs with Channel Limits Considering Pre-existing SCADA and PMU Measurements.”

[18]A. Deswal, D. K. Jain, and M. Singh, “State estimation through optimally placed PMU,” Proc. 6th IEEE Power India Int. Conf. PIICON 2014, 2015.

[19]Y. Yang and S. Roy, “PMU placement for optimal three-phase state estimation performance,” 2013 IEEE Int. Conf. Smart Grid Commun. SmartGridComm 2013, pp. 342-347, 2013.

[20]K. Mazlumi, H. Vahedi, and S. M. Ezzati, “Optimal Placement of PMUs in Power Systems Using Heuristic Algorithms and Mixed Integer Non Linear Programming Methods,” Electrical Engineering, 2010. [Online]. Available: http://ieeexplore.ieee.org/document/5491599/.

[21]S. Chakrabarti, E. Kyriakides, and D. G. Eliades, “Placement of Synchronized Measurements for Power System Observability,” IEEE Trans. Power Deliv., vol. 24, no. 1, pp. 12-19, Jan. 2009.

[22]S. Azizi, A. S. Dobakhshari, S. A. Nezam Sarmadi, and A. M. Ranjbar, “Optimal PMU Placement by an Equivalent Linear Formulation for Exhaustive Search,” IEEE Trans. Smart Grid, vol. 3, no. 1, pp. 174-182, Mar. 2012.

[23]C. M. Akachukwu, A. M. Aibinu, M. N. Nwohu, and H. B. Salau, “A Decade Survey of Engineering Applications of Genetic Algorithm in Power System Optimization,” in 2014 5th International Conference on Intelligent Systems, Modelling and Simulation, 2014, pp. 38-42.

[24]Z. J. Liu, M. Y. Wang, and D. D. Wang, “Application of Scaling Genetic Algorithms Using MapReduce in Optimizing the Configuration of PMU,” no. Ciced, pp. 10-13, 2016.

[25]G. N. Korres, P. S. Georgilakis, N. C. Koutsoukis, and N. M. Manousakis, “Numerical observability method for optimal phasor measurement units placement using recursive Tabu search method,” IET Gener. Transm. Distrib., vol. 7, no. 4, pp. 347-356, Apr. 2013.

[26]A. Yda Amira and G. Fathi, “Optimal PMU placement for full network observability case of the tunisian network,” in Eighth International Multi-Conference on Systems, Signals & Devices, 2011, pp. 1-5.

[27]P. Gopakumar, M. J. B. Reddy, and D. K. Mohanta, “Novel multi-stage simulated annealing for optimal placement of PMUs in conjunction with conventional measurements,” in 2013 12th International Conference on Environment and Electrical Engineering, 2013, pp. 248-252.

[28]B. Rajasekhar and A. K. Chandel, “Joint placement of phasor and power flow measurements for power system observability using differential evolution,” in 2013 International Conference on Power, Energy and Control (ICPEC), 2013, pp. 489-494.

[29]T. K. Maji and P. Acharjee, “Multiple solutions of optimal PMU placement using exponential binary PSO algorithm,” in 2015 Annual IEEE India Conference (INDICON), 2015, pp. 1-6.

[30]J. Peppanen, T. Alquthami, D. Molina, and R. Harley, “Optimal PMU placement with binary PSO,” in 2012 IEEE Energy Conversion Congress and Exposition (ECCE), 2012, pp. 1475-1482.

[31]J. Wang, C. Li, and J. Zhang, “Optimal Phasor Measurement Unit Placement by an Improved PSO Algorithm,” in 2012 Asia-Pacific Power and Energy Engineering Conference, 2012, pp. 1-4.

[32]M. Hurtgen and J. C. Maun, “Optimal PMU placement using Iterated Local Search,” Int. J. Electr. Power Energy Syst., vol. 32, no. 8, pp. 857-860, 2010.

[33]S. Mandava, J. Vanishree, and V. Ramesh, “A spanning tree approach in placing multi-channel and minimum channel PMU’s for power system observability,” vol. 5, no. 3, pp. 518-524, 2015.

[34]Q. Li, T. Cui, Y. Weng, R. Negi, F. Franchetti, and M. D. Ilic, “An Information-Theoretic Approach to PMU Placement in Electric Power Systems,” IEEE Trans. Smart Grid, vol. 4, no. 1, pp. 446-456, Mar. 2013.

[35]H. A. Abdelsalam, A. Y. Abdelaziz, and V. Mukherjee, “Optimal PMU placement in a distribution network considering network reconfiguration,” in 2014 International Conference on Circuits, Power and Computing Technologies [ICCPCT-2014], 2014, pp. 191-196.

[36]P. Prabhakar and A. Kumar, “Voltage stability assessment using Phasor Measurement technology,” in 2014 IEEE 6th India International Conference on Power Electronics (IICPE), 2014, pp. 1-6.

[37]A. Raj, “Optimal PMU Placement by Teaching-Learning Based Optimization Algorithm,” pp. 1-6.

[38]N. H. A. Rahman, A. F. Zobaa, and M. Theodoridis, “Improved BPSO for optimal PMU placement,” Proc. Univ. Power Eng. Conf., vol. 2015-Novem, pp. 1-4, 2015.

[39]C. Paper, T. Indore, and T. Indore, “Optimal PMU Placement using Best First Search Algorithm with Pruning,” no. May, pp. 1-2, 2016.

[40]H. H. Müller and C. A. Castro, “Optimal substation PMU placement method for the two-level state estimator,” 2013 3rd Int. Conf. Electr. Power Energy Convers. Syst. EPECS 2013, pp. 2-7, 2013.

[41]P. Mohammadi and S. Mehraeen, “PMU Optimal Placement using Sensitivity Analysis for Power Systems Fault Location,” pp. 244-249, 2015.

[42]H. Kazemi Karegar and M. Dalali, “Optimal PMU placement for full observability of the power network with maximum redundancy using modified binary cuckoo optimisation algorithm,” IET Gener. Transm. {&} Distrib., vol. 10, no. 11, pp. 2817-2824, 2016.