Miniature Wireless Inertial and Magnetic Sensors Research

“An object in motion tends to stay in motion unless an external force acts upon it. Similarly, if the object is at rest, it will remain at rest unless an unbalanced force acts upon it.”

“When a force acts on an object, it will cause the object to accelerate. The larger the mass of the object, the greater the force will need to be to cause it to accelerate.”

• Sir Isaac Newton.

Throughout centuries, people were fascinated with the study of motion. In fact, several disciplines were created, in which laws of physics and mechanics are applied to objects or biological systems in order to study the effect of the forces acting upon them. One of those disciplines is biomechanics, which involves, among others, the study of the kinetics and kinematics of the human body.

Locomotion is one of the primary functions of the human body (Moore et al. 2010) and studying its characteristics and its effects on the musculoskeletal system is of great importance, especially in our times, when musculoskeletal disorders are ranking very high amongst the top debilitating diseases worldwide, according to the World Health Organisation (Brooks 2006; Cross et al. 2014; St. John 2015).

Degenerative musculoskeletal diseases, such as osteoarthritis (OA) are most prevalent in the elderly population, of 55 years and older (Reginster 2002). Over the past decades, the United Nations reported a steady increase in the life expectancy of the world population (Oeppen and Vaupel 2008), which marked a concomitant increase in the number of years in which sufferers need to manage the disease (Cross et al. 2014), thereby not only lowering the quality of life of the patient but also putting extra strain on the health care system.

Although OA is an autoimmune disease and its origins are not yet fully understood, the literature suggests that in some patients OA can be caused by other degenerative processes such as femuroacetabular impingement (FAI) (Benedetti et al. 1998; Ganz et al. 2001), genu varum or genu valgum (Moore et al. 2010), which have a much earlier onset than OA. Early diagnosis in such cases could help prevent or postpone the onset of OA in the patient’s joints. Motion analysis has been widely tested as a means of diagnosing skeletal misalignment processes, such as the ones mentioned above.

The knee joint is not only the largest joint in the human body, but due to its position and weight bearing properties, also one of the most injurie and disease prone skeletal feature (Moore et al. 2010). After all, knee OA is one of the most prevalent types of arthritis affecting the world population (Cross et al. 2014). Moreover, the knee joint is often used in proof of concept studies, as a simplified biomechanical hinge joint (Seel et al. 2014), which only allows rotation about its main axis – the flexion – extension axis, making it ideal for the purpose of the current study. The motion to be analysed in the following chapters will be knee flexion-extension during dynamic walking conditions.

Amongst the most popular motion analysis tools are the marker based optical motion capture systems and their associated protocols. Optical motion capture is often performed in the laboratory with very expensive equipment and using this type of equipment in a non-laboratory based environment presents significant limitations which can compromise the accuracy of the acquired data. However, the differences between the laboratory setting and a natural environment in which a movement is carried out could affect the manner in which the patient conducts himself.

It is therefore of great importance to find an appropriate motion analysis tool which can be used accurately in a non-laboratory based environment, is user friendly, requires a short set up time and is cost effective.

The scope of the current thesis is to combine the use of state of the art equipment and a motion capture and computational data processing protocol which allows biomechanical analysis of human motion in a non-laboratory based environment.

The purpose of the study is to test the applicability, feasibility and reliability of using a network of wireless inertial sensors and a designated data acquisition and processing protocol to assess human knee flexion-extension during gait in a non-laboratory based environment.

Successfully proving that using such a technique in a non-laboratory based environment is applicable and reliable, could not only offer an ambulatory, and more rapid, user friendly, and cost effective alternative to the optical motion capture – silver standard, used currently in the laboratory, the applications of such a technique would be spread across numerous fields, e.g. diagnostics and prevention of disease, physical repair, ergonometry, engineering of prosthetic limbs.

Objectives

The objectives of the current study are to perform a series of experiments using a network of miniature wireless inertial and magnetic sensors, in conjunction with a data processing protocol, proposed by Seel et. al (2014) and described in detail in the following chapters, in order to validate the system for use in a non-laboratory based environment.

The experiments will have the following purposes:

1. Ruling out any gyroscope bias.
2. Testing the accuracy of the gyroscope sensors and the methodology proposed by Seel et. al (2014) for deriving a rotation angle from gyroscope data, against a robotic setup – gold standard.
3. Testing the accuracy with which the cameras of the optical motion capture system track the markers in the measurement volume.
4. Testing the methodology proposed by Seel et. al (2014) for calculating a rotation angle by combining gyroscope and accelerometer data, against the Vicon calibration wand.
5. Validating the above mentioned method for calculating knee flexion-extension angles during gait, against the Vicon camera system – current silver standard for human motion capture.
6. Comparing knee flexion-extension angles from gait recorded in a laboratory- and a non-laboratory based environment, with the sensor system and processed with the protocol proposed by Seel et. al (2014).

Aims

   By following these objectives, the aims of the current study are to demonstrate the following set of null hypotheses:

H₀₁ – The sensor system and proposed protocol function together with high accuracy.

H₀₂ – There are no statistically significant differences between knee flexion-extension angles recorded during gait with the sensor system, and the ones recorded with the optical motion capture system.

H₀₃ – There are no statistically significant differences between knee flexion-extension angles recorded with the sensors system in the laboratory, and the ones recorded outdoors.

Anatomy and pathology of the human knee joint

The lower limbs of the human body (Fig 2.1), are part of the appendicular skeleton (Gerhardt et al. 2012). The leg is formed of three long bones, the femur constituting the thigh bone and the tibia and fibula constituting the bones of the lower leg  (Rabuffetti and Crenna 2004).

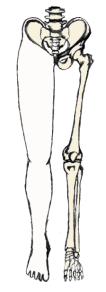
The femur (Fig 2.2A) is the largest bone in the human body. Proximally, the femur articulates with the pelvis, to form the hip joint. Distally, the femur articulates with the tibia (Fig 2.2A) to form the knee joint (Fig 2.2B)(Joseph 2014).

The femur is positioned diagonally within the thigh, forming an alignment axis along the line of force of the quadriceps femoris muscle surrounding it, which can be represented by drawing a line from the anterior superior iliac spine (ASIS) to the centre of the patella (Fig 2.2C)(Moore et al. 2010).

The tibia is almost vertically positioned within the shank, forming an alignment axis virtually parallel to the vertical gravitational axis, traversing the centre of the patella. The alignment of the knee joint is greatly influenced by the angle between the quadriceps muscle and the patellar tendon, called the Q – angle (Fig 2.2C)(Moore et al. 2010).

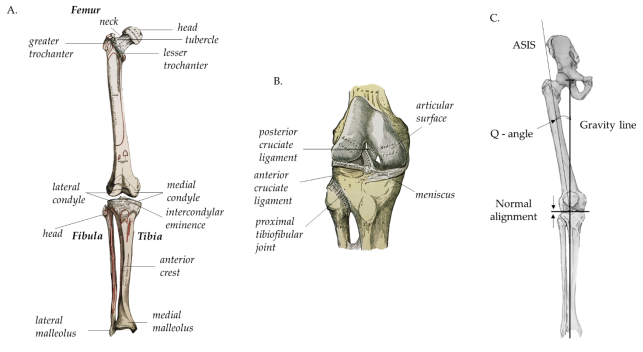
The knee joint is represented by large articular surfaces, with a joint capsule consisting of a fibrous external layer and an internal synovial membrane, lining all surfaces of the articular cavity which are not covered by hyaline cartilage (Drake et al. 2012; Moore et al. 2010) .

The hyaline cartilage, covering the bony extremities of the synovial joint, lowers friction between the elements and additional structures, such as articular discs, fat pads and tendons may be present in this type of joint (Ellis 2006).

Mechanically, the knee is a relatively weak structure, its stability being highly dependent on the strength of the soft tissue surrounding it. The most stable position of the knee joint is when a person is standing up right and the knee is fully extended. In this position, the medial rotation of the femoral condyles on the articular surface of the tibia, creates a passive lock, which is inactivated when the femur rotates laterally to allow flexion (Moore et al. 2010).

The primary functions of the human lower limbs are support and locomotion (Drake et al. 2012; Ellis 2006; Moore et al. 2010).  Functions in which the knee joints, along with the other joints of the lower limbs, play a crucial role.

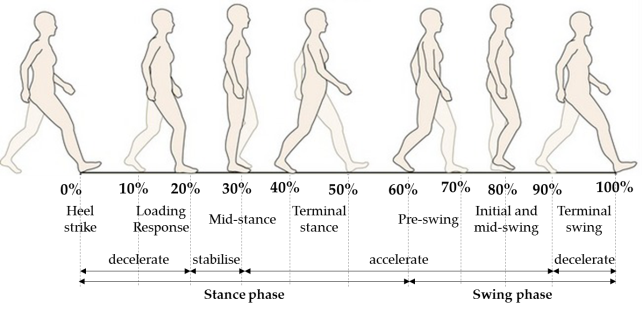
Human gait, for instance, is a complex motion which, when occurring on a planar surface, can be divided in two phases, containing 7 total events. One gait cycle (Fig 2.3) consists of a stance phase (60% of the total action) and a swing phase (40% of the total action), corresponding to a single step made by one leg.

From a biomechanical point of view, joints are often classified according to their ability to move across a defined number of axes using mechanical models. The knee joint for example is often considered to be a hinge (Fig 2.4), acting like a fulcrum between two levers, represented by the femur and tibia (Moore et al. 2010; Zatsiorsky 1998).

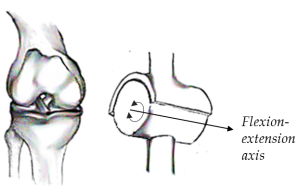
However, the movements of the knee joint are a widely discussed subject and there are at least four points of view in the literature concerning the correct identification of the flexion-extension axis of the knee joint (Zatsiorsky 1998).

The flexion-extension axis is recognized as being the main axis of rotation of the tibiofemoral joint, however, it was reported that when the knee is fully extended an endo-exo rotation of the tibia with respect to the femoral condyles occurs (Ellis 2006; Fick 1911a; Hollister et al. 1993; Moore et al. 2010). Furthermore, Hollister et al. (1993) reported that full extension of the knee is accompanied by an additional abduction-adduction of the tibia.

Firstly, based on the Reuleaux method, researchers claimed that the knee flexion-extension axis is instantaneous and displaces during motion (Blacharski and Somerset 1975; Frankel et al. 1971; Schmidt 1973; Soudan and Auderkercke 1979; Zuppinger 1904). However, this view was highly criticised by (Panjabi et al. 1982), who claimed that the flawed experimental designs of the previously mentioned researchers led to inaccuracies in their results.

Secondly, a helical rather than simple rotation occurring about a flexion-extension axis, which changes its orientation during motion, and about an independent tibial endo-exo rotation axis, was suggested (Braune and Fischer 1891; Bugnion 1892; Zuppinger 1904) and later reviewed by (Fick 1911b), (Steindler 1955), and (Strasser 1917).

However, Fick later suggested that the knee flexion-extension axis was a fixed axis located in the distal femur, traversing the lateral and medial condyle posteriorly (Fick 1911a). A hypothesis which was supported by (Elias et al. 1990) findings, which further suggested an involvement of the surrounding ligaments in the motion.

Finally, (Hollister et al. 1993) claimed that knee flexion-extension is indeed dependent on the movement of the collateral and cruciate ligaments and that therefore, mechanically, knee motion occurs about an infinite number of axes.

Nevertheless, most biomechanical models used in the literature for assessing motion capture data, assume a fixed flexion-extension axis for the knee (Cutti et al. 2010; Ehrig et al. 2007; Seel et al. 2014).

The physical aspects of the musculoskeletal system are, however, not the only factors concerning skeletal kinematics. On a physiological level, although often considered invariable, bones undergo constant remodelling under the influence of mechanical stimuli. Bone remodelling is, in fact, a constant balance between osteogenesis (the process of bone formation) and osteoclastogenesis (the process of bone resorption), processes which regulate bone mass and are highly dependent on mechanical stress and strain (Marieb 2009).

The effects of mechanical stimuli on the skeletal environment have been extensively studied in the past and mathematical models, such as Frost’s “mechanostat”, based on the theory that the human skeleton evolves for and serves mechanical needs primarily (Frost 1987), have been developed for a better understanding of this mechanism.

In Frost’s view, the skeleton has an in-built mechanical feedback system which responds to increase or decrease in mechanical loading or hormonal changes by adjusting the bone mass so that it is specially distributed for optimal mechanical function (Frost 1987).

Although Frost’s mathematical model took into account very important parameters, such as Young’s modulus for bone, peak strain, peak stress and changes in density, it did not take into account the ability of bone cells to adapt to the environment (Turner 1999).

However, Turner’s mathematical theory for bone biology, called ” the principle of cellular accommodation” (Turner 1999), based on Wolff’s “law of bone transformation” (Wolff 1982) and Frost’s “mechanostat” (Frost 1987), offered an alternative version, which corrected for flaws discovered in the initial models (Turner 1999).

In 1982, Julius Wolff proposed a theory which stated that high stress-generated potentials can act as electrical stimuli for the activation of osteocyte cells within bone tissue, which in response could trigger an anabolic event following activation of bone forming cells (Wolff 1982).

Turner’s “principle of cellular accommodation” corrected for the assumption  in Frost’s “mechanostat” that suggested that cellular sensitization is a continuous and endless process, that can eventually lead to complete loss of bone mass or ossification of bone tissue (Turner 1999).

In contrast to that, the “principle of cellular accommodation” stated that mechanical loading and unloading indeed stimulates bone formation and, respectively bone resorption, but that, over time the bone cells become immune to loading cycles (provided the load has an equal value over time) and their metabolic rate decreases.

Nevertheless, mechanical stress and strain are not exclusively affecting the bones within the skeletal system, but also the cartilage and surrounding tissue. Changes in the mechanical environment or properties of cartilage within a joint, can generate stimuli, which initiate degenerative processes (Boyd and Ronsky 1997; Churchill et al. 1998b; Davis and DeLuca 1996), e.g. osteoarthritis.

OA is a progressive disorder, which causes the loss of articular cartilage, exposing the joint extremities, where the direct contact between bones results in ulceration and calcification of the tissue.

OA is one of the world’s leading debilitating diseases, which lowers the quality of life and can lead to immobility of the patient. The exact mechanism of OA is not clear yet, however, there are a series of factors which researchers found to play a role in the onset, incidence and epidemiology of the disease.

For knee OA, these factors include amongst genetic background, age, gender, obesity (Felson 2004a), and occupational (Cooper et al. 1994; Maetzel et al. 1997; McMillan and Nichols 2005) or sports injuries (Roos et al. 1994), local mechanical factors affecting the integrity of the joint, such as muscle weakness, damage to the ligaments and meniscus, joint incongruity and misalignment of femoral condyles on the tibial plateau (Felson 2004b).

It has been reported that knee injury in men and obesity in women are amongst the leading and most modifiable causes of onset or progression of knee OA (Felson et al. 2000). Moreover, (Felson 2013) claimed that knee OA is almost always caused by increased forces acting on a joint and that such forces could be a result of knee malalignment (Felson and Hodgson 2014) or a combination of malalignment and obesity (Felson et al. 2004). Causes which can be addressed and treated in order to prevent progression or onset of OA, if identified in timely manner (Felson and Hodgson 2014; Teichtahl et al. 2009).

Genu varum (bowed-legs) and genu valgum (knocked-knees) are both conditions in which the alignment of the knee is affected. Genu varum is defined by a decreased Q-angle (Moore et al. 2010), and is reported to increase mechanical loading in the medial knee compartment by 70-79% (Tetsworth and Paley 1994) even in cases where the varum is as little as 5°, which can lead to substantial cartilage loss (Sharma et al. 2008; Teichtahl et al. 2009) and the onset of OA (Brouwer et al. 2007).

In contrast, genu valgum is defined by an increased Q-angle (Moore et al. 2010), which is reported to in increases loading in the lateral knee compartment, thereby, increasing the risk of progressive OA 5 fold (Sharma et al. 2001; Teichtahl et al. 2006).

Furthermore, (Hsu et al. 1990) and (Kettelkamp et al. 1976) report a correlation between medial lateral forces and knee alignment during standing which, however, is only present in genu varum sufferers during gait (Harrington 1983).

Motion analysis has proved to be a useful tool in the study of lower limbs kinematics and disorders of knee (Andriacchi et al. 1983; Berchuck et al. 1990; Draganich et al. 1991; Kettelkamp et al. 1976; Noyes et al. 1992; Wang et al. 1990) and increasingly more researchers use motion capture systems and biomechanical computational models for the purpose of quantifiable and numerical motion analysis (Alexander and Andriacchi 2001; Bonci et al. 2015; Cappozzo et al. 2005; Cereatti and Della Croce 2006; Cutti et al. 2010; Davis et al. 1991; Ehrig et al. 2007; Ferrari et al. 2010a; Garofalo et al. 2009; Haid and Breitenbach 2004; Kratzenstein et al. 2010b; Leardini et al. 2005; Luinge et al. 2012; Pasciuto et al. 2015; Roetenberg et al. 2003; Schepers et al. 2010; Seel et al. 2014; Taylor et al. 2005).

Motion capture systems and protocols

During the past decades, quantifiable motion analysis has been widely studied and the need for developing a low cost and user friendly technique, which enables motion capture in a non-laboratory based environment, has been emphasised time and time again (Calliess et al. 2014; Gaffney et al. 2011; Liu et al. 2011; Pfau et al. 2005; Soangra and Lockhart 2012; Vlasic et al. 2007; Wixted et al. 2010; Yang et al. 2011; Zhou and Hu 2004, 2008).

Quite a few motion capture systems were developed in order to aid motion studies. These systems were reviewed extensively (Frey et al. 1996; Hightower and Borriello 2001; Meyer et al. 1992; Welch and Foxlin 2002) and can be largely classified in the following categories: robot aided, visual and non-visual (Vlasic et al. 2007; Zhou and Hu 2004, 2008).

• Robot aided motion capture

This technique employs the use of electromechanical systems, such as Gypsyâ„¢ (Meta Motion) and ShapeWrapâ„¢ (Measurand), called exoskeletons, which the subjects are required to wear, in order to compute joint angles from electric resistance. These systems are not restricted to laboratory use, however, they are uncomfortable and motion restricting even in the most updated versions of the hardware (Vlasic et al. 2007).